(ISSN 1430-6972)
IP-GIPT DAS=09.11.2014 Internet-Erstausgabe, letzte Änderung: 19.01.20
Impressum: Diplom-Psychologe Dr. phil. Rudolf Sponsel Stubenlohstr. 20 D-91052 Erlangen
Mail: sekretariat@sgipt.org. _ Zitierung & Copyright
Anfang Autokorrelation_Datenschutz_ Überblick Relativ Aktuelles_ Rel. Beständiges_Titelblatt _Konzept _Archiv _Region _ Service iec-verlag _Wichtige Hinweise zu Links und Empfehlungen
Willkommen in unserer Internet-Publikation für Allgemeine und integrative Psychotherapie, Abteilung Wissenschaft, Bereich Statistische Methoden, und hier speziell zum Thema:
Autokorrelation in Psychologie, Psychopathologie, Psychotherapie
und Wissenschaft
Kritische Darstellung und Diskussion anhand von praktischen
Beispielen
Originalarbeit von Rudolf Sponsel, Erlangen
Einführung in die Methoden
und Probleme der Autokorrelation
Autokorrelation bedeutet technisch, Teile einer Datenreihe mit der
Ausgangsdatenreihe zu korrelieren in der Weise, dass die Werte der Datenreihe
verschoben werden, indem z.B. der 2. Wert dem 1. Wert der Ausgangsreihe,
der
3. Wert dem zweiten Wert der Ausgangsreihe usw. zugeordnet wird. Die Verschiebungsabstände
nennt man "Lag". Es werden also Vorgänger mit Nachfolgern korreliert
1-2 (Lag=1), 1-3 (Lag=2), 1-4 (Lag=3), ..., 1 mit n (Lag=n-1).

Übergeordnet ist es die Idee einer geordneten
Verlaufsdatenanalyse, meist an der Zeitachse dargestellt, wobei es um die
Erkennung von Regelhaftigkeiten oder gar Gesetzmäßigkeiten in
Datenverläufen geht. Das ist natürlich für die Psychologie,
Psychopathologie und Psychotherapie genauso interessant wie für die
Wirtschaftswissenschaften oder die Medizin. Es gibt viele Methoden der
Daten(verlaufs)analyse und die mathematisch konzipierte Autokorrelation
ist nur eine - wahrscheinlich die schlechteste - für Therapieverläufe
wegen ihrer für Therapien unrealistischen Annahmen der Stationarität.
Methodisch setzen die üblichen
und keineswegs ausgezeichneten Autokorrelationskonzepte Stationarität
- selbst ein ausgesprochen problematisches Konzept - , nämlich Parameterkonstanz
über "die Zeit" voraus, die in den allermeisten Fällen
in der Psychologie oder Psychotherapie nicht gegeben sein dürfte.
Autokorrelation kann aber auch ohne abenteuerliche Stationaritäts-
und Ergodizitätsannahmen
mit der Produkt-Moment-Korrelation gerechnet werden, wie unten gezeigt
wird.
Die Annahme, dass die Zeit überhaupt eine Rolle
in Entwicklungen spielen kann ist bei genauer Betrachtung mehr als problematisch,
vgl. meine Arbeit Die Zeit als Variable.
Als tatsächlich wirkende Variable spielt die Zeit nur in wenigen
Lebensbereichen, z.B. in finanzwirtschaftlichen Kontexten eine Rolle (Zins,
Mieten, Pachten, Renten). Die meisten Sachverhalte sind nicht von der Zeit
abhängig, sondern sie finden in der Zeit oder der Zeit
entlang
statt und können an Zeitachsen
dargestellt
werden.
Meist bleibt unbegründet und offen in der Literatur,
was Autokorrelation genau für einen Sinn und Nutzen haben soll und
warum nicht die gewöhnliche Produkt-Moment-Korrelation auf die Berechnung
der Vorgänger-Nachfolger-Korrelation angewendet werden kann oder man
sich auf eine Analyse der Ausgangsdatenreihe beschränkt, weil der
Graph der Rohwerte ja meist schon sehr viel sagt. Sinnvoller und viel einfacher
dürfte ohnehin die einfache Analogmethode der Mustererkennung für
Verlaufssegmente sein. Ich werde das später in einer eigenen Arbeit
Daten-Verlaufs-Analyse
aufgreifen.
In dieser Arbeit sollen daher ein paar Fragen zur
Autokorrelation und Zeitreihenanalyse problematisiert werden: Wozu kann
man Autokorrelationen oder Zeitreihenanalysen in der Psychologie, Psychopathologie
und Psychotherapie gebrauchen? Sind die methodischen Voraussetzungen erfüllbar?
Welche Aussagen sind über die Autokorrelationen zusätzlich möglich?
Gibt es nicht viel sinnvollere und einfachere Methoden der Verlaufsdatenanalyse?
Nun, die obige Bestimmung Korrelation der Vorgänger
und Nachfolger in einer Datenreihe ist recht abstrakt, betrachten wir daher
zunächst ein konkretes und praktisches Beispiel aus der Psychotherapie,
wie es sich Tausende von Malen alljährlich ereignet:
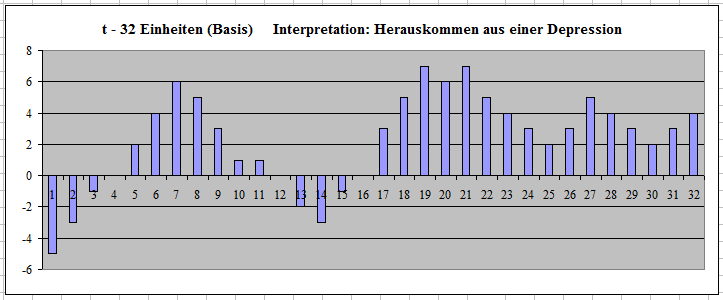
Beispiel 01a Datenverlauf
Herauskommen aus einer Depression - 32 Zeiteinheiten, z.B. als Wochenwerte
Eine Depression kann durch folgende Symptome
oder Syndrome im wesentlichen
erfasst werden: Antriebshemmung, schwarze Stimmung (bis hin zur inneren
Versteinerung), kognitive Beeinträchtigungen (Aufmerksamkeit, Denken,
Gedächtnis) und einige andere, z.B. psychosomatische Symptome. Im
folgenden Beispiel ist eine bipolare Skala mit dem theoretischen Bereich
-9 bis +9, die tatsächlich erfassten Werte reichen hier von -5 bis
+7:
Beispiel 01b Graph der Verschiebung der Daten um eine Position (Lag=1)
Zunächst der Graph für Lag=1, d.h. um genau eine Verschiebung. Der zweite Wert der Ausgangsreihe rückt an die Stelle des 1. Wertes der zweiten Reihe:
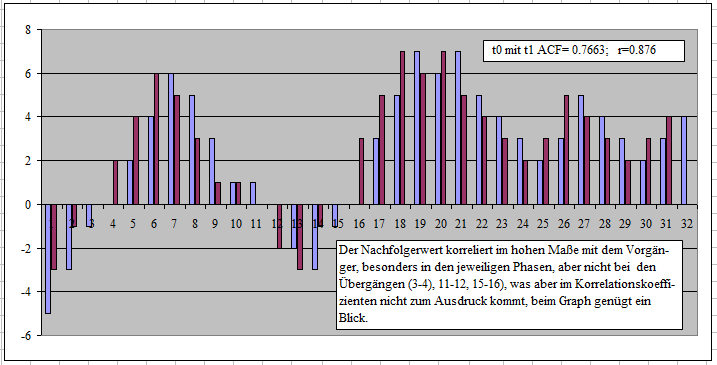
Wie man sieht, muss die Korrelation zwischen Vorgänger und jeweiligem Nachfolger relativ hoch sein. Wie man auch sieht, braucht man hierfür aber keine Autokorrelation, sondern das lässt sich mit bloßem Augenschein oder auch quantitativ mit der "normalen" Produkt-Moment-Korrelation nach Bravais & Pearson, also mit dem üblichen metrischen Korrelationskoeffizienten sehr gut erfassen, wie im Folgenden belegt wird. Aber nicht einmal das braucht man letztlich, es genügt im Grunde die bloße Verlaufsdarstellung, wenn man an einer genaueren quantitativen Bestimmung nicht interessiert ist.
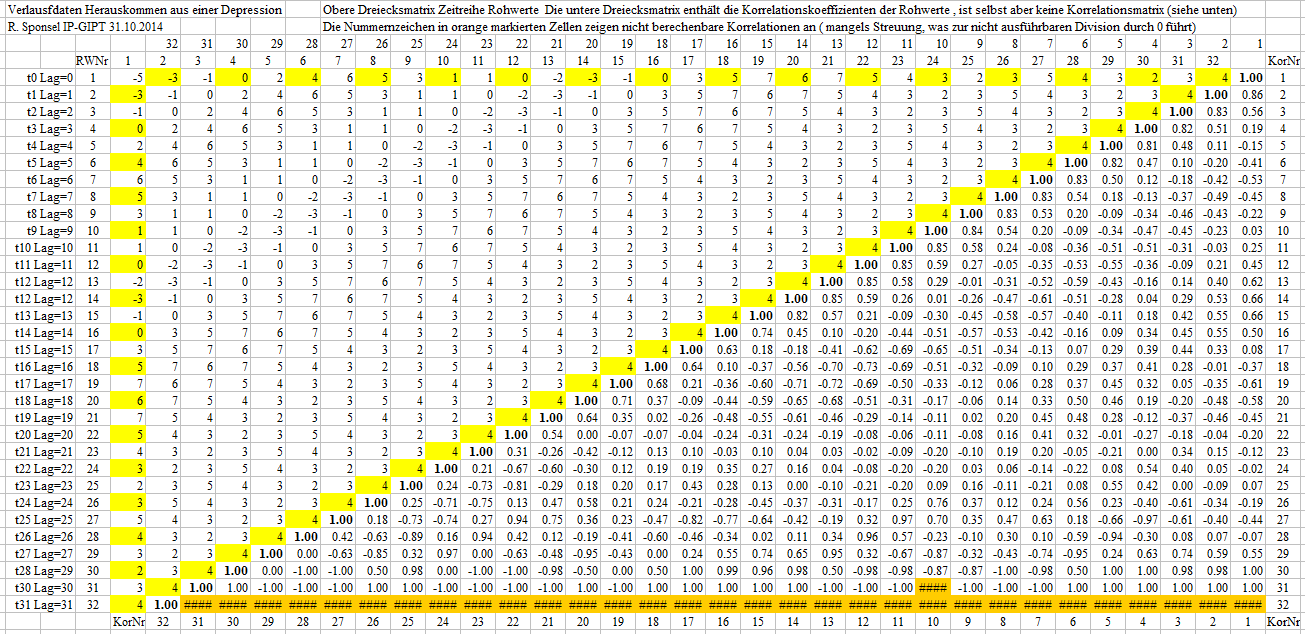
Beispiel 01c Graphen der Verschiebung der Daten um die Positionen oder Lags 2, 3, ... 31
Warnung: Die untere rechte Dreiecksmatrix enthält zwar korrekt gebildete einzelne Korrelationskoeffizienten, aber sie beruhen auf jeweils unterschiedlichen Stichprobenumfängen, so dass die Anordnung in einer Matrix in aller Regel keine multivariate Weiterverarbeitung erlaubt, weil die so erstellte Matrix nicht positiv semidefinit (alle Eigenwerte >= 0) ist, wovon man sich im Folgenden auch überzeugen kann. Die Matrix sieht zwar von 1-30 ganz typisch und harmlos aus, aber sie entgleist extrem, wenn man sich die extrem hohen negativen Eigenwerte dieser Matrix anschaut (unten, orange markiert).
_
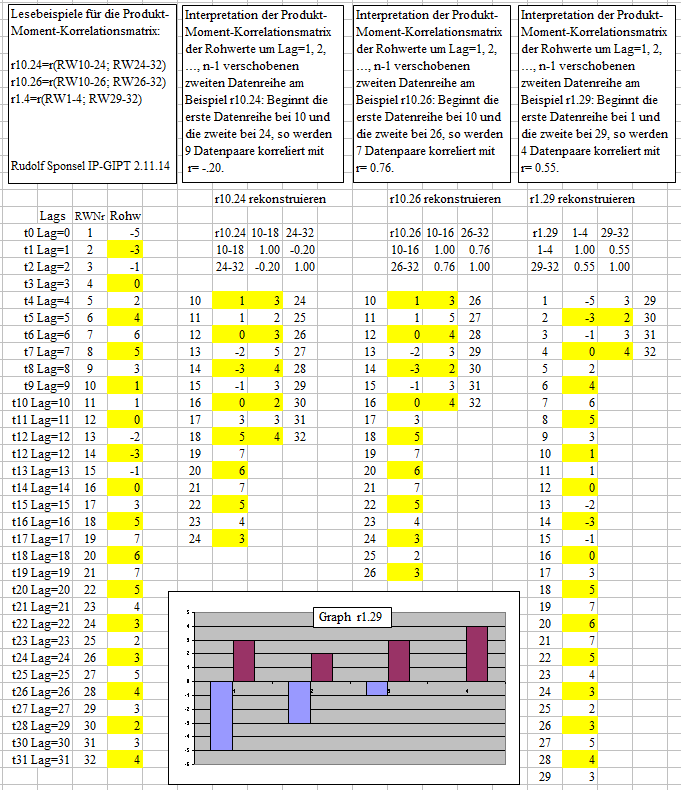
- Lesebeispiele
der Produkt-Moment-Matrix
_
Exkurs: Demonstration der Entgleisung der Matrix, wenn sie fälschlich als Korrelationsmatrix interpretiert wird (obwohl sie so aussieht)
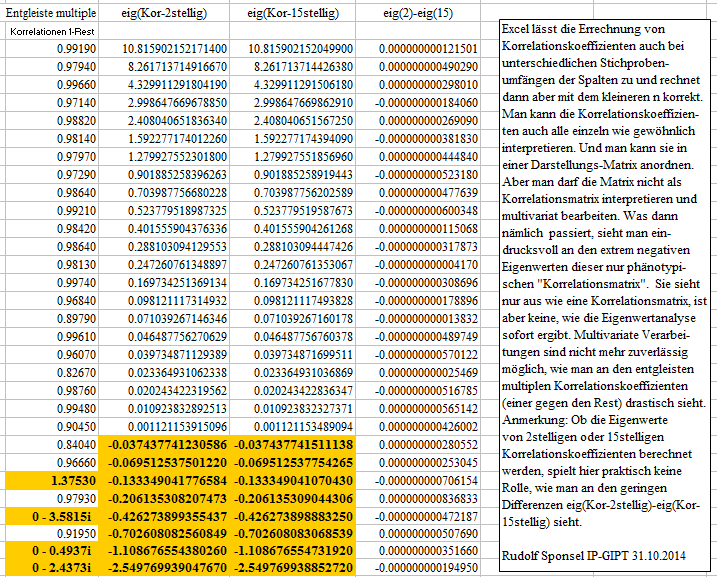
Von den multiplen Korrelationskoeffizienten (einer gegen den Rest) entgleisen vier, wobei drei abenteuerliche imaginäre Werte annehmen und einer deutlich mit 1.3753 entgleist.
Und von den negativen Eigenwerten sind einige exorbitant jenseits von Gut und Böse angesiedelt. Obwohl jeder einzelne Korrelationskoeffizient in der Tabelle korrekt gebildet wurde und alle ihrem Werte nach zwischen -1 <= r <= +1 liegen und die Matrix wie eine Korrelationsmatrix aussieht, ist sie keine, denn dazu müsste sie positiv semidefinit, d.h. alle Eigenwerte >= 0 sein. Die Summe der Eigenwerte, 30, entspricht der Ordnung 30, die gerechnet werden konnte.
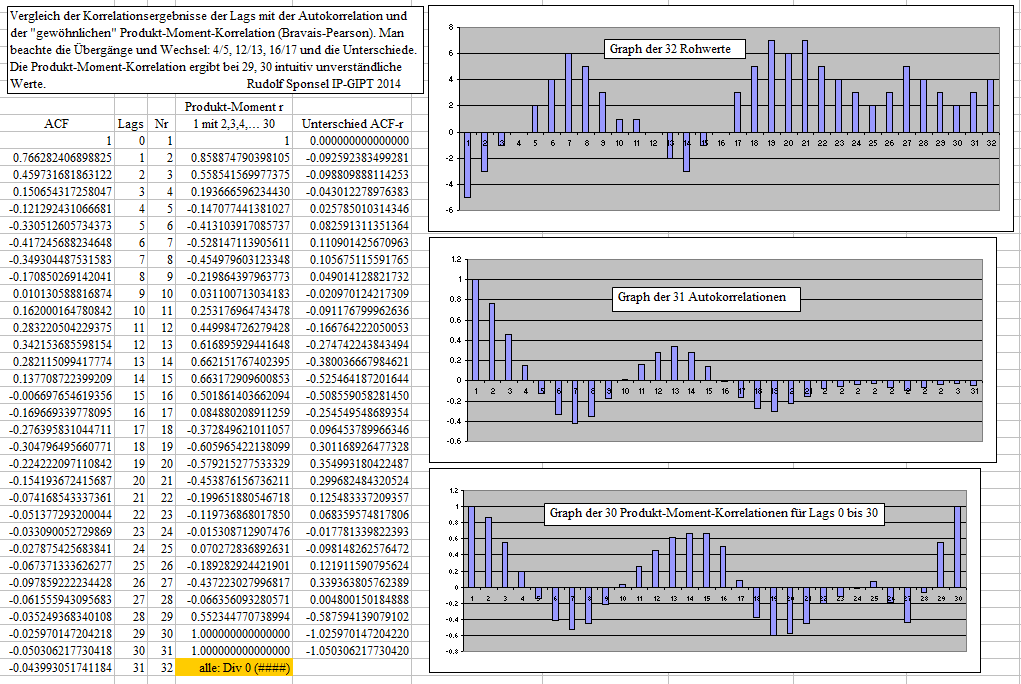
Vergleich Vorgänger-Nachfolger-Auto-Korrelation mit dem Produkt-Moment-Korrelationskoeffzienten
_
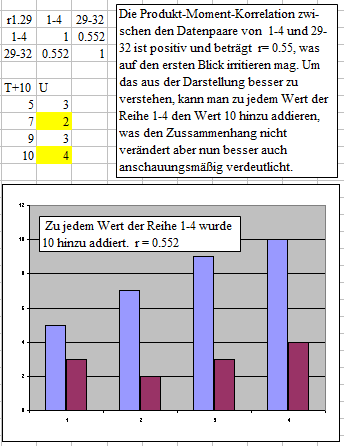
Zur Erklärung der Unterschiede ab Lag 29
 |
_
_ _ _ _ _ _ _ Man sieht, dass sich die Korrelations- koeffizienten teilweise erheblich un- terscheiden, überdeutlich bei Lag 29 und 30, wo die Produkt- Moment- Korrelation der Anschauung nach schwer verständliche positive Korrelationen liefert. Der Grund bei Lag 30 liegt in einer verborgenen linearen Abhängigkeit, was zur Korrelation 1 führt. Der Grund für die positive Korrelation bei Lag=28 (Verlaufswert 29) ist auf den ersten Blick intuitiv irritierend, skaliert man etwas um, wird es aber auch anschauungsmäßig verständlich. |
Stationarität in der Wissenschaft
Stationarität wurde als Konzept in der mathematischen Statistik
entwickelt. Es bedeutet dort kurz und bündig Parameterkonstanz - z.B.
der Momente (Mittelwert, Varianz, Kovarianz, Schiefe, Exzess, ...) über
die Zeit. Man entwickelte Verfahren, die unter diesen Voraussetzungen anwendbar
sind. Dazu gehört auch die Autokorrelation, die in der Technik und
Signalverarbeitung offenbar mit Gewinn eingesetzt wird. Doch wieso sollte
Parameterkonstanz gelten? Und was soll es überhaupt heißen,
wenn "die Zeit" keine Rolle spielt? Sie spielt ja in den seltensten Fällen
eine Rolle (> die Zeit als Variable),
der Verlauf von Werten wird nur an der Zeitachse dargestellt,
aber die Werte selbst sind ja keine Wirkung der Zeit. Der Mensch stirbt
ja nicht am Zeitvergehen, sondern am Zell- und Funktionsverfall seiner
Organe. Die Aktien steigen oder fallen nicht, weil die Zeit vergeht, sondern
weil Anleger sich zum Kaufen oder Verkaufen entscheiden. Sofern die Zeit
eine echte Variable wird, spielen meist Konventionen eine Rolle, z.B. bei
Zins, Pacht, Miete, Rente u.a.m. Was bedeuten dann Lebens- und Verfallsdauern?
Die man ja berechnen kann, wie nützlich zeigen die Versicherungen,
z.B. Lebenserwartungsberechnungen. Hier werden ganz offensichtlich Zeitpunkte
oder Zeiträume bestimmt. Ist die Zeit also doch eine Variable? Jein.
Wenn sie sehr eng mit Prozessen korreliert, so kann man "die Zeit" als
Quasivariable betrachten, in die sich sehr viele unterschiedliche Prozesse
"hineinverdichten".
- Exkurs: Ist die Zeit eine Moderator- oder Pseudovariable? (>
die
Zeit als Variable)
Ein Zusammenhang zwischen A und B kann durch C, D, ... begründet sein. C, D, ... heißen dann Moderatorvariablen. Erfasst man die Stimmung (Y) eines Menschen im zeitlichen Verlauf (X) und interpretiert man X als Zeitachse, so hängt Y nicht von der Zeit ab, sondern ihr Verlauf wird nur in der Zeit oder an der Zeitachse dargestellt. Die Zeit selbst bewirkt nichts, aber die Wirkungen all der Variablen, die die Stimmung beeinflussen, modulieren oder erzeugen die Wirkung, die an der Zeitachse dargestellt werden kann. Ist die Zeit nun eine vermittelnde, eine Transport-, also eine Moderatorvariable oder ist sie nur eine Hilfs- oder Pseudovariable, wenn auch oft von hohem praktischen Nutzen? Viele Entwicklungen können z.B. zum Alter in Beziehung gesetzt werden.
Schlittgen & Streitberg (1984), S. 79 schreiben über Stationäre
Prozesse:

Kreiß, Jens-Peter & Neuhaus, Georg (2006) zur Stationaritäts-Annahme.

Halten wird fest: Stationarität ist eine sehr starke Annahme,
die in vielen Fällen fragwürdig und problematisch ist. In der
Wissenschaft sollen aber möglichst keine Annahmen getroffen,
sondern geprüft und kontrolliert werden, ob sie berechtigt sind oder
nicht.
Stationarität in Psychologie, Psychopathologie und Psychotherapie am Beispiel Depression und Wohlbefinden
Zusammengefasst: Das (Er-) Leben ist nicht stationär, sondern wechselhaft und unbeständig. Es wird zwar von Zufällen beeinflusst, aber die meisten Erlebens- und Verhaltensweisen sind keine Realisationen von "Zufallsvariablen", sondern Ergebnisse regelgelenkter oder nachvollziehbarer Prozesse.
Die meisten Arbeiten in der Psychologie, Psychopathologie
und Psychotherapie über Autokorrelationen sind unkritisch, formalistisch
und gehen auf die inhaltlichen Probleme gar nicht ein - wie üblich
bei den SzientistInnen. Manche sind auch nur inkonsequent wie z.B. Schmitz
(1987, S. 85), wenn er schreibt (fett-kursiv RS):
- "6.1.2 Psychologische Bedeutung von Stationarität
Die inhaltliche Bedeutung dieses Konzepts ist einfach. Der Prozeß ändert im gesamten Verlauf seinen Level und seine Variabilität sowie seine interne Zeitstruktur nicht. Durch die Stationaritätsforderung werden zunächst gerade die für die Psychologie besonders bedeutsamen Prozesse von einer Betrachtung ausgeschlossen. Prozesse, in denen Veränderung stattfindet, sind für alle psychologischen Teildisziplinen gleichermaßen von Bedeutung. Oftmals sind gerade Art und Ausmaß der Änderung besonderer Gegenstand von Untersuchungen: Habituation und Adaptation, Lernen und Vergessen, Wachstums- und Abbauprozesse oder Neukalibrierung (siehe Kap. 3). Besonders die Untersuchung entwicklungspsychologischer Fragestellungen führt sehr häufig zu Verläufen, die nicht stationär sind. Hier sind vor allem auch die Stufen- und Phasenmodelle zu nennen, bekannt sind die von KROH (1951), FREUD (1940) und PIAGET (1948). Um nicht eine Vielzahl psychologischer Fragestellungen von einer zeitreihenanalytischen Betrachtung von vornherein auszuschließen, gibt es verschiedene Möglichkeiten (siehe Kap. 6.1.6). Es bleibt festzuhalten, daß das statistische Stationaritätskonzept in Zusammenhang mit psychologisch besonders bedeutsamen Sachverhalten zu sehen ist."
- Der letzte Satz ist angesichts der Vorausführungen dunkel, unverständlich
und inkonsequent.
Eine Depression ist wie das Wohlbefinden keine Wirkung der Zeit,
sondern sie ereignet sich in der Zeit und man kann ihren
Verlauf auf einer Zeitachse eintragen und darstellen. Meist ändert
sie sich im Zeitverlauf, wobei diese Änderung wiederum gar nichts
mit der Zeit zu tun hat, sondern was in dieser Zeit durch
die depressionserzeugenden oder depressionserhaltenden bzw. wohlbefindenerzeugenden
oder wohlbefindenerhaltenden Faktoren geschieht.
Die meisten Depressionen verlaufen einerseits ähnlich,
andererseits ganz unterschiedlich. Typologisch, orientiert an den Klassifikationssystemen
sind folgende grundlegende Verlaufselemente erfasst: Hochs, Tiefs, Normalbereich,
Übergänge und Wechsel, die langsam oder plötzlich erfolgen
können.
Phasen, die nur aus Hochs bestehen heißen in starker Ausprägung
manisch und in überdurchschnittlicher Ausprägung hypomanisch.
Phasen fortgesetzter Tiefs heißen depressiv und sehr stark Tiefs,
die oft einen stationären Aufenthalt erfordern, schwer depressiv.
Wie kann man eine Depression oder Wohlbefinden in
einen Zahlenwert abbilden? Die Beantwortung dieser Frage fällt in
das Gebiet der Psychopathometrie und Psychologie. Und hier in das komplizierte
Feld der Mess- und Skalentheorie. Die "einfachste" Möglichkeit ist,
Symptome, Schweregrade, Verläufe und Dauern zu erfassen. Dabei entstehen
meist keine metrischen Skalenwerte, aber auch mehr als bloße Ordinalwerte.
Die Stevens-Klassifikation taugt nicht für die psychologisch-psychotherapeutische
Praxis. Das Problem ist bislang nicht gelöst. Aber die Grundidee von
Fuzzy-Zahlen zeigt die richtige Richtung. Wir brauchen "Zahlen" und Messwerte,
die der Realität der Psychologie, Psychopathologie und Psychotherapie
entsprechen und keine szientistische Numerologie in streng mathematischer
Verkleidung.
Prüfung der Stationaritätsannahme
Gedacht ist ein Datenverlauf in der Zeit d(t1, t2, ...tn). Die Stationaritätsannahme besagt, dass es keine Rolle spielt, welcher Ausschnitt betrachtet wird, weil wesentliche statistische Parameter wie Mittelwert und Varianz über den gesamten zeitlichen Verlauf als gleich angenommen werden. Nun ist "annehmen" nicht sehr wissenschaftlich und unbefriedigend. Man muss in den Veröffentlichungen ziemlich suchen, um Aussagen zu finden, die die Prüfung der Stationarität zum Gegenstand haben.
Revenstorf (1979), S. 58 nennt folgende Kriterien: "Nichtstationarität erkennt man zunächst an grossräumigen Schwankungen des Niveaus der Zeitreihe (vgl. Abbildung 2.4b). Ausserdem hat die Autokorrelationsfunktion bei nichtstationären Modellen einen besonders flachen Verlauf. ..."
Schmitz (1987), behandelt das Problem in Kap. 6 "Nichtstationärität
und divisive Prozeßanalyse". Wie oben schon zitiert, S. 85, "6.1.2
Psychologische Bedeutung von Stationarität.
Die inhaltliche Bedeutung dieses Konzepts ist einfach. Der Prozeß
ändert im gesamten Verlauf seinen Level und seine Variabilität
sowie seine interne Zeitstruktur nicht. ..."
Schmitz nennt auch Tests.
Als einfachstes praktisches Kriterium kann vielleicht dienen: Stationäre
Prozesse sind durch eine gewisse zufällige Gleichförmigkeit über
den ganzen Verlauf charakterisiert. Unser Depressionsbeispiel oben ist
sozusagen ein klares Gegenbeispiel.
Literatur (Auswahl)
- Anderson (1994) The statistical analysis of time series. John Wiley and Sons.
- Box, G. E. P. & Jenkins, G. M. (1970 ff) Time Series Analysis - Forecasting and Control. San Francisco: Holden Day.
- Bredenkamp, Jürgen & Feger, Hubert & (1983, Hrsg.) Hypothesenprüfung. Enzyklopädie der Psychologie Themenbereich B Methodologie und Methoden, Serie 1 Forschungsmethoden der Psychologie, Bd. 5. Göttingen: Hogrefe.
- Gruber, Antje Birgit (2011) Kointegration in Theorie und Praxis: Statistische Analyse gemeinsamer Entwicklungstrends in psychologischen Zeitreihensystemen. Dissertation [PDF]
- Horne, G. P., Yang, M. C. K. und Ware, W. B. (1982) Time series analysis for single-subject designs. Psychological Bulletin, 1982, 91, 178-189.
- Jaglom, A. M. (dt. 1959). Einführung in die Theorie der stationären Zufallsfunktionen. Berlin: Akademie.
- Karrenberg, U. (2012) Signale - Prozesse - Systeme. Eine multimediale und interaktive Einführung in die Signalverarbeitung. 6. A. Berlin: Springer. Anmerkung: Eingegliedert ist DASYLab 11, eine speziell für den Lernen entwickelte Software der Messdatenerfassung und Messdatenanalyse, so dass viele Beispiele in dem Buch hiermit gerechnet und anschaulich dargestellt werden können.
- Keeser, W. (1979) Zeitreihenanalyse in der klinischen Forschung. Ein empirischer Beitrag zur Box-Jenkins-Methodologie. München: Dissertation.
- Krauth, J. (1980) Possible misinterpretations when evaluating psychological time series. Archives of Psychology, 1980, 133, 139-147.
- Kreiß, Jens-Peter & Neuhaus, Georg (2006) Einführung in die Zeitreihenanalyse. Berlin: Springer.
- Möbus, Claus & Nagl, Willy (1983) Messung, Analyse und Prognose von Veränderungen. In (229-470) Bredenkamp, Jürgen & Feger, Hubert & (1983, Hrsg.) [Stationarität wird im Sachregister nicht aufgeführt]
- Kupfer, J., Brosig, B. & Brähler, E. (2005). A multivariate time-series approach to marital interaction. GMS Psycho-Social-Medicine, 2 , 1 - 10.
- Petermann, F. & Hehl, F.-J. (1979). Einzelfallanalyse — ein Überblick. In: Petermann, Franz & Hehl, Franz Josef (1979, Hrsg.), l-16.
- Revenstorf, Dirk (1979) Zeitreihenanalyse für klinische Daten. Methodik und Anwendungen. Weinheim: Beltz.
- Schlittgen, Rainer & Streitberg, Bernhard H. J. (1984) Zeitreihenanalyse. München: Oldenbourg.
- Smith, J. D., Handler, L. & Nash, M. R. (2010) Therapeutic assessment for preadolescent boys with oppositional defiant disorder: A replicated single-case time-series design. Psychological Assessment, 22 (3), 593 - 602.
- Schmitz, Bernhard (1987) Zeitreihenanalyse in der Psychologie. Verfahren zur Veränderung und Prozeßdiagnostik. Weinheim: Deutscher Studien Verlag.
- Schneider, Matti & Mentemeier, Sebastian (2010) Zeitreihenanalyse mit R [PDF]
- Stroe-Kunold, Esther (2005) Multivariate Analyse instationärer Zeitreihen: Integration und Kointegration in Theorie und Simulation. Diplom-Arbeit Psychologisches Institut Heidelberg. [PDF]
- "Googeln" ergibt sehr viele Ergebnisse, oft aber wenig praktisch und
meist auch unkritisch.
Glossar, Anmerkungen und Endnoten: > Eigener wissenschaftlicher Standort.
1) GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
__
Tests
- Augmented Dickey-Fuller
Test [W]
__
Box-Pierce Test (Schneider, Matti & Mentemeier, Sebastian (2010) Zeitreihenanalyse mit R [PDF] , S. 26)
__
Ljung-Box Test (Schneider, Matti & Mentemeier, Sebastian (2010) Zeitreihenanalyse mit R [PDF], S. 26)
__
Rao-Tintner-Test (Schmitz 1987, S. 85)
__
Spearman-Rang-Autokorrelationen Angabe von Schmitz 1987, S. 211.
__
Tests und Test-Ideen
Augmented Dickey-Fuller Test, Box-Pierce Test, Ljung-Box Test, Rao-Tintner-Test, Turning Point Test,
Datenreihe in Segmente zerlegen und auf Parameter-un-gleichheit testen.
Von welchen anderen Faktoren können die Parameter abhängen?
Gibt es zu der betrachteten möglicherweise komplexen Variable überhaupt Parameter oder greifen hier nicht viele ineinander?
__
Turning Point Test (Schneider, Matti & Mentemeier, Sebastian (2010) Zeitreihenanalyse mit R [PDF], S. 27)
Standort: Autokorrelation.
*
Korrelation. Was bedeutet der lineare Korrelationskoeffizient?
Autokorrelation in Psychologie und Wissenschaft. *
Die Zeit als Variable, Zeitdiagramme, Zeitreihenanalysen. Was bedeutet die Zeit als Variable?
(Semi) Indefinite Pseudo-Korrelationsmatrizen.
Einfache Berechnung der multiplen Korrelationen nach Tucker et. al.
Überblick Statistik in der IP-GIPT.
Fast- Kollinearität in Korrelationsmatrizen mit Eigenwertanalysen erkennen.
Partielle Korrelationen: Definition und Methode, Tücken und Fallen , Wichtige Anwendungen in der Psychologie, Kombinatorik der Anzahlen. * Standard-Matrix-Analyse (SMA) und Nicht-Linearitäts-Paradox in Korrelationsmatrizen * Systematische Veränderungs-Paradoxie * Vollständige 501 partielle Korrelationsanalysen am Beispiel IST 70 * Wissenschaft in der IP-GIPT * Kritik Handhabung Faktorenanalyse * Numerisch instabile Matrizen und Kollinearität in der Psychologie * Fehlersimulation und Faktorenanalyse * Zahlen * Der Kardinal-Skalenbeweis zur Summen-Score-Funktion * Grundzüge einer ideographischen Wissenschaftstheorie * Welten *
Beweis und beweisen in der Statistik * Signifikanztest *
*
| Suchen in der IP-GIPT,
z.B. mit Hilfe von "google": <suchbegriff>
site: www.sgipt.org
z.B. Korrelation site: www.sgipt.org. |
Dienstleistungs-Info.
*
Zitierung
Sponsel, Rudolf (DAS). Autokorrelation in Psychologie, Psychopathologie, Psychotherapie und Wissenschaft. Kritische Darstellung und Diskussion anhand von praktischen Beispielen IP-GIPT. Erlangen: https://www.sgipt.org/wisms/statm/kor/Autoko/autokor.htm
Copyright & Nutzungsrechte
Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das direkte, zugriffsaneignende Einbinden in fremde Seiten oder Rahmen ist nicht gestattet, Links und Zitate sind natürlich willkommen. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus ... geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.
Ende Autokorrelation _Datenschutz_Überblick _ Relativ Aktuelles _ Rel. Beständiges _ Titelblatt _ Konzept _ Archiv _ Region _ Service iec-verlag _ Mail: _ sekretariat@sgipt.org _
Änderungen wird gelegentlich überarbeitet, ergänzt und vertieft * Anregungen und Kritik willkommen
15.11.14 Korrektur zur Summe der Eigenwerte der Pseudokorrelationsmatrix.