(ISSN 1430-6972)
IP-GIPT DAS=07.09.2003 Internet-Erstausgabe, letzte Änderung: 02.09.23
Impressum: Diplom-Psychologe Dr. phil. Rudolf Sponsel Stubenlohstr. 20 D-91052 Erlangen
Mail: sekretariat@sgipt.org_Zitierung & Copyright
Anfang _Beweis in der Mathematik_Datenschutz_Überblick_Rel. Aktuelles _Rel. Beständiges _Titelblatt_ Konzept_ Archiv_ Region_Service_iec-verlag__Wichtiger Hinweis zu Links und zu Empfehlungen
Beweis und beweisen in Mathematik und Logistik
Blicke über den Zaun zum Auftakt für eine psychologisch-psychotherapeutische
Beweislehre
aus allgemein integrativer psychologisch-psychotherapeutischer
und einheitswissenschaftlicher
Sicht
Einführung, Überblick, Verteilerseite Beweis und beweisen
von Rudolf Sponsel, Erlangen
Hinweis: Wenn nicht ersichtlich werden (Externe
Links) in runden und [interne IP-GIPT
Links] in eckige Klammern gesetzt, direkte Links im Text auf
derselben Seite sind direkt gekennzeichnet.
In dieser Übersichtsarbeit wird das Thema im Überblick gesamtheitlich
aus einheitswissenschaftlicher Perspektive dargestellt. Im Laufe der Zeit
folgen weitere Ausarbeitungen.
- Einstieg Beweis und beweisen in Mathematik und Logistik.
- Zwei Beispiele: Chinesischer Beweis zum Pythagoras aus dem 11. Jhd.
- Euklids Primzahlbeweis.
- Das Problem des Tertium non datur beim indirekten Beweis.
- Gefährliche Regionen und Prozeduren: wo sich besondere Vorsicht empfiehlt.
- Brouwers Denkweise und Argumentation nach Dirk von Dalen (1992).
- Ein Beispiel aus dem Netz zum Problem des Tertium non datur.
- Mann oder Nicht-Mann, das ist hier die Frage.
- "Konstruktive" Idee für die Legitimation der Anwendung des Tertium non datur.
- Erste Bedingung vollständige Disjunktion.
- Zweite Bedingung: der Aussageobjektbereich muss existieren.
- Dritte Bedingung: Das Aussageobjekt darf nicht nichtperiodisch unendlich sein.
- Bisheriges Ergebnis zum Tertium non datur.
- Anmerkung: Beweisidee wie man die Allgemeingültigkeit des Tertium non datur widerlegen könnte.
- Psychologischer Exkurs: Konträres und Kontradiktorisches.
- Mathematische Beweisregeln.
- Vollständige Induktion.
- Beweisfehler.
- Die Bedeutung der Gödel'schen Sätze.
- Exkurs I. Mathematischer und empirischer Beweis.
- Exkurs II: Das Drama der Mathematik-SchülerInnen.
- Exkurs III: Das große Problem der Mathematisierung der Welt.
- Exkurs IV: Ist die Mathematik so sicher, wie sie sich präsentiert?
- Exkurs V: Mehr oder minder gut beweisen?
- Querverweis: Rabulistik und Sophistik in der altehrwürdigen Mathematik.
- Querverweis zum Grundlagenstreit in der Mathematik.
- Literatur. * Links.
„Was beweisbar ist, soll in der Wissenschaft nicht ohne Beweis geglaubt werden.“
(Dedekind Was sind und sollen die Zahlen? 1872, Vorwort erster Satz).
Einstieg Beweis und beweisen in Mathematik und Logistik

;-) Was für ein Beweisverfahren wird hier angewendet?
Das Beweisideal wurde in der Geschichte der Mathematik
bereits sehr früh erreicht. Obwohl Euklid als genialer Großmeister
mathematischer Beweiskunst gilt, berichtet z.B. Schwarz von einem beeindruckenden
chinesischen
Beweis zum Satz des Pythagoras aus dem 11. Jhd. v. Chr. (!)
Zum Wesen der (reinen) Mathematik gehört, alles
und jedes zu beweisen, was behauptet oder benutzt wird. Das sollte im Grunde
aber ganz allgemein das Prinzip Wissenschaft sein, die MathematikerInnen
wenden es - neben den LogistikerInnen als vermutlich
einzige - nur äußerst, ja geradezu 'gnadenlos' konsequent an,
wenn auch für die Außenstehenden oft nur schwer nachvollziehbar.
MathematikerInnen und mathematische AnwenderInnen unterscheiden sich daher
mit wenigen Ausnahmen meist durch
ihr Interesse und ihre Fähigkeit, beweisen zu können, wobei das
mathematische Beweissystem allerdings nicht so klar vermittelbar ist, wie
es wünschenswert erscheint. Man kann sogar sagen, die Mathematik unternimmt
viel, um es ihren
SchülerInnen
schwer zu machen. Das ist sehr schade, weil dadurch die Vorbild- und
Idealfunktion der Mathematik nicht in der wünschenswerten Weise genutzt
werden kann.
Reine Mathematik beschäftigt sich zweckfrei
und nur erkenntnisinteressengeleitet mit mathematischen Objekten und ihren
Beziehungen mit dem Ziel, alles Mögliche zu beweisen; Anwendungsfragen
- mit Ausnahme der Astronomen und Physiker - werden eher als fremd oder
störend erlebt. Die AnwenderIn ist üblicherweise nicht an Beweisen,
sondern wie ihr Name ja schon kund tut, am Anwenden interessiert, obschon
es für die einheitswissenschaftliche
Entwicklung wünschenswert und schön wäre, wenn sich die
Beweisidee allgemein durchsetzte, was nur funktionieren kann, wenn sie
allgemein, didaktisch, praktisch und anwendungsorientiert entsprechend
aufbereitet und vermittelt wird.
Zwei Beweisbeispiele aus der Mathematik
Ich verstehe nicht viel von Mathematik, was mich aber nicht darin hindert, selbständig zu denken. Relativ zu meinem 'Niveau und Verständnis' habe ich zwei Beispiele ausgewählt, von denen ich glaube, daß sie besonders geeignet sind, die mathematische Denkweise und ihre Beweisverfahren eindrucksvoll zu vermitteln.
Chinesischer Beweis aus dem 11. Jhd. v. Chr. zum Satz des Pythagoras (aus Schwarz, S. 6-7):
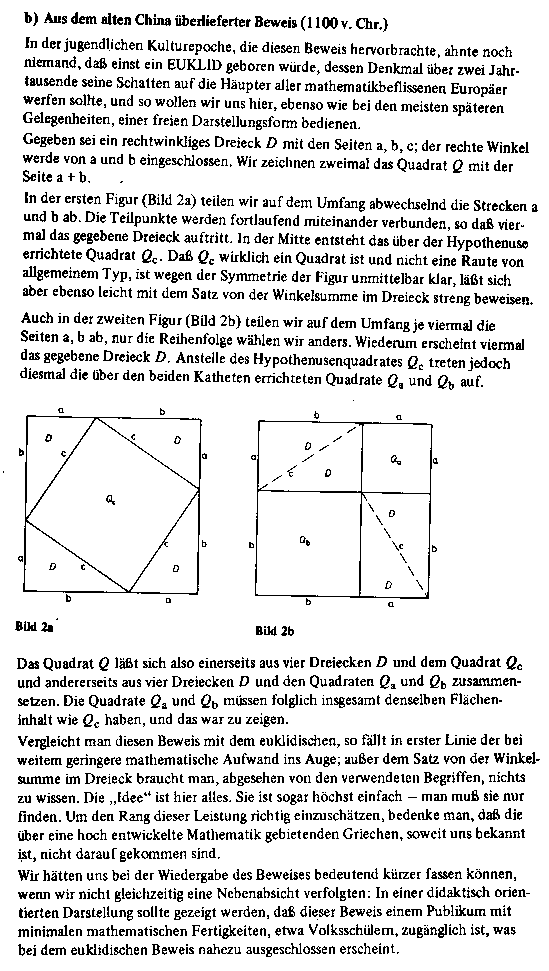
Primzahlbeweis von Euklid
Zunächst sei kurz das in der Mathematik häufig anzutreffende Beweisverfahren des indirekten Beweises skizziert:
Ein indirektes
Beweisschema aus dem Netz (Uni-Erlangen)
"Etwas rezeptologischer klingt das Vorgehen bei indirekten Beweisen
etwa so:
- Beim indirekten Beweis nehmen wir die Verneinung der Behauptung an und kennzeichnen sie als Annahme.
- Die Annahme führen wir zu einem Widerspruch.
- Beim Erreichen des Widerspruches wissen wir: Die Annahme war falsch.
- Es gilt die Verneinung der Annahme, also die Behauptung."
Unter Primzahl verstehen die MathematikerInnen Zahlen >1, die nur
durch sich selbst oder durch 1 teilbar sind, also 2, 3, 5, 7, 11, 13, 17,
19, ... Der Beweis hat es in sich und erscheint mir sehr geeignet, die
mathematische Denkweise zu demonstrieren, nach hrz.uni dortmund Kurse Propaedeutikum
Finden:
| "Ein Beispiel soll dies an einem Problem
verdeutlichen, mit dem sich schon Euklid eingehend beschäftigt hatte.
Es geht dabei um die Fragestellung, ob es unendlich
oder nur endlich viele Primzahlen gibt.
Ein direktes Mittel wäre ein Konstruktionsprinzip, mit dem man immer größere Primzahlen angeben könnte. Also z.B. f(x)=x2+x+41 ergibt für x aus [0;39] Primzahlen, aber eben nicht darüber hinaus. Euklid bewies, daß es unendlich viele Primzahlen gibt, indirekt. Er behauptete also zunächst (Annahme): "Es gibt endlich viele Primzahlen"; diese seien p1, p2, ..., pn, wobei pn die größte Primzahl sei. Das Produkt aller dieser Primzahlen plus 1 (dies sei Z) ist mit Sicherheit größer als pn, kann von daher (nach der Annahme) keine Primzahl sein. Z müßte sich dann aber als Produkt einer Primzahl p (aus der Menge p1, .., pn; andere gibt es ja nicht) und einem Restfaktor r darstellen lassen: Man müßte also beide Seiten durch p ohne Rest teilen können. Doch bei Z läßt sich ein solches p als Faktor nicht finden: bleibt doch bei der Division von Z durch jede der Primzahlen p1, .., pn immer ein Rest 1.Z = p * r Da die Annahme zum Widerspruch führt, gilt: "Es gibt unendlich viele Primzahlen." (q.e.d.: quod erat demonstrandum)" |
Das Problem des Tertium non datur beim indirekten Beweis
Die Annahme der allgemeinen Gültig- und Anwendbarkeit des tertium
non datur: A ist entweder wahr oder falsch, ein Drittes gibt es
nicht - könnte nur als Axiom gelten, wenn es denn allgemein einsichtig
wäre, was offensichtlich nicht der Fall ist, wie der mathematische
Grundlagenstreit_beweist
;-). Allgemein einsichtig ist wohl, daß man jeweils nur versuchen
kann, Aussagen als wahr oder falsch zu erweisen. Das kann glücken
und kann scheitern. Es hat nun den Anschein, als ob viele MathematikerInnen
einen "Zaubertrick" pflegten, der indirekter Beweis heißt, der eine
allgemeine Gültigkeit des tertium non datur für alle mathematischen
Objekte, ihre Merkmale und Beziehungen voraussetzt. Das kann man zwar beschließen,
aber ob die Tatsachen immer den Beschlüssen gehorchen, mag doch -
gerade auch in der Mathematik - sehr bezweifelt werden. Ein solches Dogma
erscheint doch eher zweifelhaft, wissenschaftsfremd und daher im Grunde
eigentlich unmathematisch. Andererseits
weist Erhard Schmidt in seiner Rektoratsrede "Über Gewißheit
in der Mathematik", 1930, (Meschkowski 1990,
S. 242), in der er sich mit der intuitionistischen Position und dem
Grundlagenstreit
auseinandersetzt, darauf hin (farbig unterlegte Hervorhebung durch mich):
- "Die intuitionistischen Angriffe lassen sich nicht
widerlegen. Aber ein gewisses Gefühl sagt dem mathematischen Bewußtsein,
daß man bei einem Beweise unter uneingeschränkter Benutzung
des Tertium non datur vielleicht gewisse Behauptungen passieren muß,
deren Sinn ungeklärt ist, aber niemals zu verifizierbar falschen Resultaten
gelangen wird - ein Gefühl, das von der Erfahrung bestätigt wird.
| Denn in der gewöhnlichen klassischen Mathematik, die sich, wie schon gesagt, uneingeschränkt des „Tertium non datur" bedient, ist noch nie ein verifizierbarer Fehler zutage getreten. |
- Aber in das Reich der Mathematik haben Gefühl und Erfahrung ohne
den Paß eines Beweises keinen Zutritt, Plausibilität und Denkgewöhnung
sind keine zureichenden Ausweise."
Haben die "Klassiker" doch recht und die Auseinandersetzung um die
Gültigkeit des Tertium non datur ist 'nur' ein intuitionistisch-mathematischer
Sturm im Wasserglas?
Anmerkung:
Hilbert: Beweis des Tertium non datur: http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002508443.
Ackermann, Wilhelm (1925) Begründung des ,,tertium non datur"
mittels der Hilbertschen Theorie der Widerspruchsfreiheit. Mathematische
Annalen / Zeitschriftenband (1925) / Artikel / 1 - 36: http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002270129.
Gefährliche
Regionen und Prozeduren: wo sich besondere Vorsicht empfiehlt
| Wie es scheint, gibt es einige kritische
Gebiete, die auch von allgemeinem Beweis- Interesse sind, wo besonders
aufzu-
passen ist: 1) strenges Auseinanderhalten von Objekt- und Metaebenen auch bei der Begriffsbildung (z.B. Allmenge). 2) Strikte Unterscheidung von alle und jeder. 3) Antinomisch- paradoxe Problematik des Reflexivitätsbegriffs (kann etwas Teilmenge von sich selber sein; eine Menge sich selbst "enthal- ten"?). 4) Aussagen über Unendliches oder/ und nicht tatsäch- lich Konstruier- oder Widerlegbares. 5) Aussagen, die Gebiete betreffen, in denen es womöglich Lücken gibt; die nicht über- schaubar sind. 6) Aussagen über Gegenstandsbereiche, die nicht vollständig disjunkt oder nicht kontradiktorisch (sondern z.B. konträr) sind (das Problem kann auch bei Lücken und an allen Rändern oder Grenzen auftreten). |
Beispiele: Allmenge, Unendliches
Pseudodisjunkt: Entweder a>0 oder a<0 Gibt es eine größte (kleinste) Zahl (im Intervall i)? 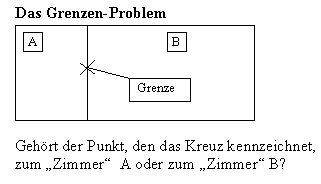
Diese Suggestivfrage ist sehr problematisch. Denn die Grenzlinie zwischen A und B kann sowohl zu A als auch zu B, also zu beiden gehören. Eine tertium non datur Forderung wäre mit dieser Deutung falsch. |
Querverweis: Aus
dem Wörterbuch der Logik: konträr und kontradiktorisch.
Querverweis: Materialien
zur Kontroverse um das Unendliche * Unendlich
Begriffe * Cantor-Probleme *
Brouwers Denkweise und Argumentation nach Dirk von Dalen (1992)

Ein Beispiel aus dem Netz zum Problem des Tertium non datur:
"Das Problem des Tertium non datur. Wir konnten uns in der Vergangenheit davon überzeugen, dass Aussagen wahr oder falsch sind. Wenn eine Aussage wahr ist, dann ist ihre Verneinung falsch; und wenn eine Aussage falsch ist, dann ist ihre Verneinung wahr. Eine dritte Möglichkeit gibt es nicht (Satz vom ausgeschlossenen Dritten, tertium non datur). Wie sieht es nun mit der Aussage ,,Der gegenwärtige König von Frankreich hat eine Glatze" und ihrer intuitiven Verneinung ,,Der gegenwärtige König von Frankreich hat keine Glatze" aus? Einer der beiden Sätze muss wahr sein, der andere falsch. Welcher ist wahr, welcher falsch? Geht man nun der Reihe nach alle Dinge durch, die eine Glatze haben, wird man unter ihnen den gegenwärtigen König von Frankreich nicht finden (denn Frankreich hat keinen König). Der Satz ,,Der gegenwärtige König von Frankreich hat eine Glatze" wäre demnach falsch. Geht man alle Dinge durch, die keine Glatze haben, dann wird man jedoch auch nicht auf den gegenwärtigen König von Frankreich stoßen. Der Satz ,,Der gegenwärtige König von Frankreich hat keine Glatze" wäre somit nicht weniger falsch! Wir stehen damit vor dem Problem, dass sowohl ein Satz als auch seine Verneinung falsch ist. Das ist nicht nur nicht einsichtig, sondern vor allem mit unserer logischen Sprache nicht verträglich." Quelle: http://logik.phl.univie.ac.at/~chris/skriptum/node60.html
Mann
oder Nicht-Mann, das ist hier die Frage
Gehen wir von einer naiven LogistikerIn aus
und nehmen wir an, für diese gäbe es nur zwei Geschlechter (was
nicht stimmt:
IL):
Mann und Frau. Die ursprüngliche Behauptung sei: X. ist ein Mann.
Nach der Rezeptologie des indirekten Beweises verneinen wir diese Behauptung
und treffen die Annahme: (1) X. ist kein Mann, also eine Frau. (2) Angenommen
wir hätten nun bewiesen, (1) führe zu einem Widerspruch (weil
wir z.B. das Geschlechtsmerkmal 'Hoden' gefunden haben). (3) Dann 'wissen'
wir nach dem tertium non datur des indirekten Beweises: {"X. ist
kein Mann = eine Frau" ist falsch}. (4) also sagen wir: "X. ist ein Mann",
obwohl sie/ er vielleicht Hermaphrodit oder sonst was ist, jedenfalls weder
das eine noch das andere.
Das Beispiel könnte lehrreich sein, weil schon
die Grundannahmen offenbar - didaktisch bewußt - falsch gewählt
wurden, was aber immer leicht möglich ist, wenn wir einen Gegenstandsbereich
nicht richtig kennen. Daß es nur zwei Geschlechter gibt, gilt eben
nur allgemein und oberflächlich betrachtet. D.h. aber im Prinzip,
wenn wir die Welt nicht richtig und schon gar nicht vollständig kennen,
was meist der Fall sein dürfte, dann dürfen wir auch keine Annahmen
dergestalt machen, daß die Merkmalswelt in genau zwei Klassen, M+
und M- erschöpfend und vollständig zerfällt.
Idee
für die Legitimation der Anwendung des Tertium non datur
Die Grundvoraussetzung ist, dass es genau und nur zwei Wahrheitswerte
"wahr" und "falsch" gibt, kein dazwischen, kein weder noch, kein unentschieden,
kein non liquet.
Erste Bedingung
vollständige Disjunktion
Das vorherige Beispiel führt zu einer "konstruktiven" Idee, wann
das
tertium non datur gerechtfertigt sein könnte. Dann nämlich,
wenn der Merkmalsbereich genau und vollständig erschöpfend in
zwei echte Merkmals-Klassen, M+ und M- zerlegt werden kann, wenn also eine
vollständige
Disjunktion gilt, z.B.: Jede natürliche Zahl ist entweder
gerade oder ungerade. Kann man für eine Zahl n zeigen, daß sie
nicht gerade sein kann, darf zu Recht geschlossen werden, sie muß
ungerade sein.
| Wendet man diese Idee auf den Primzahlbeweis von Euklid an, müßte der indirekte Schluß hier erlaubt sein, wenn jede natürliche Zahl entweder Primzahl oder keine Primzahl ist und es ein Drittes nicht gibt: wenn sich also die natürlichen Zahlen vollständig und erschöpfend in die zwei Klassen aufteilen lassen: Primzahlen und Nicht-Primzahlen. |
| Behauptung: Der allgemeine Schluß, aus nicht-wahr (nicht-falsch) folge real falsch (wahr), ist falsch. Aus nicht-wahr (nicht-falsch) folgt real gar nichts, außer der Tautologie, nicht-wahr (nicht-falsch) ist nicht-wahr (nicht-falsch). Das Beispiel, entweder gilt: a>0 oder a<0, demonstriert unmittelbar, daß hier keine vollständige Disjunktion vorliegt und daher falsch sein muß (für a=0). Nun kann man zwar eine zweiwertige Logik mit dem Axiom des tertium non datur als Modell einer Welt zugrundelegen, ob aber dieses Modell im jeweiligen betrachteten Fall sinnvoll und gerechtfertigt ist, das wäre zu zeigen. Daß eine Aussage in allen möglichen Welten wahr oder falsch sein muß, gemahnt daher nicht an Wissenschaft, sondern an Metaphysik und Theologie. Im Grunde wäre dies ein Forschungsgebiet für die allgemeine Wissenschaftstheorie aber auch für die jeweiligen Fachwissenschaften: unter welchen Bedingungen darf man das teritium non datur anwenden und wo nicht? |
- Anmerkung:
Beweisidee
wie man die Allgemeingültigkeit des Tertium non datur widerlegen könnte
Könnte man beweisen, daß wir nicht alle Eigenschaften a) der Zahlen und b) ihrer Beziehungen kennen und unser Wissen Lücken hat, sollte bewiesen sein, daß das tertium non datur nicht allgemein gültig sein kann und darf, nämlich überall dort nicht, wo unser Wissen - oder auch unsere Definitionsmacht - Lücken hat.
Zweite
Bedingung: der Aussageobjektbereich muss existieren
Wenn X nicht tot ist, lebt X. = Wenn X nicht tot ist, dann ist X nicht
nicht tot.
Diese Aussage oder ihre Umkehrung ist nur dann war, wenn es X gegeben
hat oder gibt.
Wenn A nicht schlecht drauf ist, dann ist A nicht nicht schlecht drauf = Wenn A nicht schlecht drauf ist, ist A gut drauf. Diese Aussage oder ihre Umkehrung ist nur dann war, wenn es A gegeben hat oder gibt.
Dritte
Bedingung: Das Aussageobjekt darf nicht nichtperiodisch unendlich sein
Wenn x gerade ist, dann ist x nicht ungerade.
Das lässt sich im nichtperiodischen Ziffernfall nur entscheiden,
wenn man eine endliche Integer bilden kann. Bei irrationalen Zahlen kann
man daher nie wissen, ob sie gerade oder ungerade sind.
Bisheriges
Ergebnis zum Tertium non datur
Das tertium non datur kann angewendet werden, wenn der der Prädikatsbereich
eine vollständige Disjunktion erlaubt, das Aussageobjekt existiert
(hat) und nicht nichtperiodisch unendlich ist.
Psychologischer
Exkurs: Konträres und Kontradiktorisches
Möglicherweise erschwert eine Eigentümlichkeit unserer Sprache
und Alltagslogik den Umgang mit dem Tertium non datur, nämlich das
Phänomen [konträrer
und kontradiktorischer] Gegensätze (Widersprüche). Wer
nicht unser Freund ist, ist unser Feind, so tönte vor einiger
Zeit Präsident G. W. Bush, jun. mit dem Tenor Tertium non datur.
Was
nicht schwarz ist, muß deshalb noch nicht weiß sein.
Wahr
und falsch können sowohl in konträrer als auch in kontradiktorischer
Bedeutung Anwendung finden. Konzipiert man es kontradiktorisch, ist zu
zeigen, daß die [Welt], auf die es
angewendet wird, entsprechend kontradiktorisch 'aufgebaut' ist bzw. modelliert
wird.
Hilbert: Beweis des Tertium non datur: Digitalisierungs-Zentrum
Uni Göttingen.
Hilbert: Axiomatisches Denken (Vortrag in Zürich am 11.9.1917.
Digitalisierungs-Zentrum Uni Göttingen.
Mathematische Beweisregeln
Vollständige Induktion
(Felgner
2012)
Vorab: Der Ausdruck ist unglücklich und irreführend, da die
mathematisch vollständige Induktion nichts mit dem induktiven Vorgehen
in den empirischen Wissenschaften zu tun hat. Nach Auffassung der Mathematiker
ist es ein deduktives Verfahren. Das Prinzip oder die Beweisregel der sog.
vollständigen Induktion ist eine spezifisch-typisch mathematische
Methode. Sie ist nicht einfach zu verstehen, wenn auch oft das Gegenteil
behauptet wird. Die Beweisregel der vollständigen Induktion wird meist
wie folgt formuliert (> siehe):
- Man zeige, dass die Behauptung für 1 gilt.
- Man zeige, dass die Behauptung für n+1 gilt unter der Voraussetzung, dass sie für n wahr ist.
Ist das Verfahren zirkulaer
?
Die Regel 2 mutet zirkulär an, denn man will ja nicht beweisen,
dass n+1 gilt unter der Voraussetzung, dass es für n
richtig ist, sondern dass es allgemein für n richtig ist, was in dieser
Beweisregelformulierung aber ausdrücklich vorausgesetzt wird. Überspitzt:
Man beweist dann, dass etwas richtig ist, was man als richtig vorausgesetzt
hat. Diese Frage wird in den von mir eingesehenen Ausführungen nirgendwo
erörtert oder problematisiert, obschon sie ja von der Formulierung
des Beweisverfahrens auf der Hand liegt. Das finde ich merkwürdig
und ein wenig beunruhigend. Solange ich keine nachvollziehbare Erklärung
für dieses Problem gefunden habe, sehe ich die bisher von mir eingesehehen
Begründungen als unzureichend an. Meine eigenen Überlegungen
hierzu sind noch nicht genügend entwickelt.
Irritationen
um die Beweisbarkeit des Axioms
Obwohl meist gesagt wird, das vollständige Induktionsprinzip sei
ein Postulat oder Axiom, wird mancherorts auch behauptet, es sei beweisbar
(> Versuche).
Man fragt sich dann natürlich, wozu man ein Axiom braucht, wenn der
Satz beweisbar ist?
Versuche,
die vollstaendige Induktion zu beweisen
Felgner (2012) berichtet von Frege und Dedekind, ich habe selbst Versuche
gefunden bei Thiele
S. 132; oder in Behnke
et al. S. 172 für endliche Mengen. Felgner berichtet auch, dass sich
Peano aus dem Streit, ob das Prinzip der vollständigen Induktion beweisbar
ist oder nicht, herausgeholten habe.
Formulierungen der vollstaendigen Induktion
Aus Der kleine Duden
Mathematik (1986), S. 448t:

Felgner (2012) formuliert das Prinzip der vollständigen Induktion wie folgt:

Beispiel Summenformel
s=n(n+1)/2
Im Internet gibt es mehrere Beispielsammlungen, die man mit Suchmaschinen
leicht finden kann. Ich gebe inzwischen ungern Links an, weil die URL-Adressen
sehr häufig sehr instabil sind, keine Weiterleitungen vorsehen und
daher vielfach Fehlermeldungen 404 hervorrufen, an denen ich nicht interessiert
bin.
Beispiel
zur Summenformel aus Schwarz (1975) - wo auch das Prinzip erläutert
wird.
5.1 in diesem Text 1+2+3+...+n = n(n+1)/2

Beweisfehler
Meinel & Mundhold (2009) schreiben (S.62): "Typische Fehler beim Beweisen sind:
- unzulässiges Argumentieren mit Beispielen,
- Verwendung gleicher Symbole zur Bezeichnung verschiedener Dinge,
- Hantieren mit nicht exakt oder widersprüchlich definierten Begriffsbildungen,
- unzulässige Gedankensprünge beim Schlussfolgern und
- Ausnutzung von bis dahin noch unbewiesenen Behauptungen zur Begründung von einzelnen Beweisschritten.
Anmerkung: Im Wörterbuch
der Logik sind viele Beweisregelfehler aufgeführt.
Die Bedeutung der Gödel'schen Sätze
Die Bedeutung der Gödel'schen Sätze faßt kurz und bündig
nebst den Folgerungen Konforowitsch (dt. 1983) in seinem Buch Logischen
Katastrophen auf der Spur [S.
34] zusammen:
"Unerwartet und außerordentlich wichtig für
die logische Begründung der Mathematik waren zwei berühmte Sätze
des österreichischen Mathematikers KURT GÖDEL, die im Jahre 1931
veröffentlicht wurden (s. auch NAGEL/NEWMAN (1979), MESCHKOWSKI (1985)
und PETER (1984)).
Der erste Satz behauptet: Jede formalisierte und
widerspruchsfreie axiomatische Theorie, die die Arithmetik umfaßt,
ist unvollständig, das heißt, es existiert stets eine Aussage
dieser Theorie, die inhaltlich wahr ist, aber nicht aus den Axiomen der
Theorie abgeleitet werden kann.
Der zweite Satz behauptet: Es ist nicht möglich,
die Widerspruchsfreiheit einer formalisierten und widerspruchsfreien axiomatischen
Theorie, die die Arithmetik umfaßt, mit Mitteln zu beweisen, die
sich in dieser Theorie formalisieren lassen.
Folgerungen aus den GÖDELschen Sätzen
waren sehr unerwünscht für solche Gelehrten, die den Versuch
unternahmen, die Widerspruchsfreiheit axiomatischer Theorien, zum Beispiel
der Arithmetik der natürlichen Zahlen, mit besonders elementaren Mitteln
zu beweisen. Es stellte sich heraus, daß die axiomatische Methode
in der Wissenschaft nicht allmächtig ist."
Exkurs
I. Mathematischer und empirischer Beweis
Es heißt: Sätze, die in der Mathematik (richtig) bewiesen
sind, gelten - oft in den scheinbaren Gegensatz zu den empirischen Gesetzen
gestellt - immer und für alle Zeiten. Stimmt das überhaupt [Lakatos
bestreitet dies] ? Und falls, was bedeutet es und wie kommt das? Nun, ich
behaupte: sofern es stimmte, wäre es trivial. Und sofern man die Voraussetzungen,
die man in der Mathematik trifft, in die empirische Welt übertrüge,
stimmte es dort auch. Das liegt schlicht und einfach daran, wenn man in
der Mathematik bezüglich der Voraussetzungen unveränderliche
Systeme betrachtet (Aber: Grundlagenstreit).
Wenn also die Voraussetzungen und die Beweisregeln konstant bleiben, wieso
sollte sich dann jemals etwas an den Sätzen, die geschlußfolgert
wurden, ändern? Genauso kann man natürlich im Bereich der empirischen
Wissenschaften argumentieren: wenn die Naturgesetze und die Erkenntnismethoden
konstant bleiben, wieso sollte sich dann an den abgeleiteten Aussagen jemals
etwas ändern? So gilt, ganz im Sinne der einheitswissenschaftlichen
Idee: Wenn sich nichts ändert, ändert sich nichts und wenn
sich was ändert, ändert sich was, und das ist in der Mathematik
nicht anders als in den empirischen Wissenschaften oder im Alltag.
Exkurs
II: Das Drama der MathematikschülerInnen
 |
Reine oder richtige Mathematik lernen heißt gewöhnlich,
beweisen lernen und genau das lernt die Mehrheit der MathematikschülerInnen
nie. Doch schlimmer noch. Vielen wird jegliches Interesse für die
Mathematik regelrecht ausgetrieben und damit nicht selten auch ein wichtiges
Stück Selbstwertgefühl . Woran liegt das? Und muß das so
sein, kann und sollte dies geändert werden und falls wie? Stella Baruk
spricht sich leidenschaftlich für eine Änderung des Mathematikunterrichts
aus und plädiert für die pädagogische und didaktische Nutzbarmachung
der Fehler und Irrtümer, für eine andere Sprache und Haltung
den SchülerInnen gegenüber.
|
Exkurs III: Das große Problem der Mathematisierung der Welt
Wird die Welt berechenbarer, die Wissenschaft exakter und erfolgreicher
dadurch, daß Mathematik angewendet wird? Die Antwort
heißt ganz klar Jein. Es gilt wohl sicher für
die Naturwissenschaften, allen voran für Astronomie und Physik, Chemie,
Biologie, Medizin in ihrer naturwissenschaftlichen Basis, Meteorologie,
aber auch für die aus den Naturwissenschaften gewonnene Technik.
Gilt es aber auch für die Sozialwissenschaften,
etwa für das Recht, die Ökonomie, Soziologie und Psychologie?
Sicher Nein. Woran liegt das?
|
(Mathematik Modell) Relation (Anwendung Empirisches Modell) |
Durch den Erfolg in Naturwissenschaft und Technik sind die verantwortlichen
MathematikerInnen träge, nachlässig oder sogar blind für
das grundlegende Problem geworden:
| Basis-paradigmatische Gretchenfrage: Unter welchen Bedingungen darf Mathematik, bzw. genauer ein mathematisches Modell, als formale Grundlage für ein empirisches Modell dienen? |
So weit mir für die Psychologie bekannt ist, sind solche Modelle nur im Rahmen allgemeiner [Meßtheorie] - die auch wieder kaum jemand versteht - entwickelt worden.
Querverweis: Rabulistik und Sophistik in der altehrwürdigen Mathematik
Exkurs IV: Ist die Mathematik so sicher, wie sie sich präsentiert ?
Ist ein Satz erst einmal bewiesen, so soll er für immer und alle Zeiten gelten, so zumindest das Credo und Marketing der MathematikerInnen. Und deshalb gilt die Mathematik als die exakteste aller - sogar als Königin der - Wissenschaften, und das ist sie vermutlich immer noch - trotz der folgenden kritischen Ausführungen. Aber sie ist längst nicht mehr so exakt und klar, wie ihre Imagepflege und Marketing das suggerieren. Von 100 Beweisen sind womöglich 90 unklar, was die Voraussetzungen und Mittel betrifft, 9 falsch, problematisch oder lückenhaft und vielleicht einer "richtig" richtig. Das gilt auch für viele grosse Namen in der Mathematik, und das ist das eigentlich Bestürzende. Beweisen ist also nicht nur für Schüler, sondern auch für Fachkundige und selbst Koryphäen ein mitunter wirklich schwieriges Geschäft. Die meisten MathematikerInnen wissen das wahrscheinlich, aber sie dürften sich hüten, es jemals - und schon gar nicht öffentlich - zuzugeben. Es ist also nicht einfach, die Schwierigkeiten beim mathematischen Beweisen zu belegen und gar, es zu einem öffentlichen Thema zu machen. Wie lässt sich das nun beweisen ;-) ? Nun, im Prinzip ist die wichtigste Möglichkeit, die mathematische Literatur daraufhin zu untersuchen, wo Beweise als unzulänglich oder falsch angegriffen werden, wie es z.B. Lecat 1935 gemacht hat. Hier nun einige Beispiele:
- Aus der dramatischen Geschichte des [Parallelenpostulats] ergeben sich unzählige falsche Beweise. [Klügel] allein fand ja schon im Auftrag [Kaestners] in seiner meist wohl zu Recht gerühmten Dissertation 28 und ausschließlich fehlerhafte 'Beweise'.
- Poincaré [1914, S. 175] greift die "angeblichen Beweise für das Prinzip der Induktion, insbesondere diejenigen von Whitehead und Burali-Forti" an. Aber auch schon vorher, S. 154 (g e s p e r r t hier kursiv), zu einer Arbeit Hilberts 1904: "Der Schluß der Hilbertschen Abhandlung ist völlig rätselhaft, und wir wollen darauf nicht weiter eingehen. Die Widersprüche häufen sich; man merkt, wie der Verfasser eine unbestimmte Ahnung der von ihm begangenen petitio principii hat, und wie er sich vergeblich bemüht, die Lücken seiner Schlußfolgerung zu überbrücken. Das Resultat dieser Darlegungen können wir in folgender Form aussprechen: In demselben Augenblick, in dem Hilbert beweisen will, daß die Definition der ganzen Zahl durch das Axiom der vollständigen Induktion keinen Widerspruch enthält, versagen ihm die Kräfte, wie sie bei Russell und Couturat versagten, weil die Schwierigkeit zu groß ist."
- Church. Guerrerio (2002, S. 63 ): "Zwischen Herbst 1933 und Frühjahr 1934 erwies sich ausgerechnet das System von Church als nicht widerspruchsfrei."
- Cohen. Mehrere kleine, aber behebbare Fehler in Cohens Beweis zur Kontinuumshypothese (Dawson 1999, S. 194)
- Frege. Russell entdeckt die "Russell'sche Antinomie bei Frege.
- Gauß, C.F. Pieper (1984 , S. 198) berichtet: "Einleitend stellte GAUSS die Mängel der Beweisversuche seiner Vorgänger D' ALEMBERT, EULER, DE FONCENEX und LAGRANGE dar. GAUSS war sich darüber im klaren, daß auch er ein (lückenhaftes) Argument der algebraisch-geometrischen Anschauung entnommen hatte." In der zugehörigen Fußnote wird erläutert: "Der Beweis 'ist im Prinzip richtig, aber nicht vollständig' (F. KLEIN)."
- Gödel. Beweisfehler bei Gödels zahlreichen Varianten zum Beweis der Kontinuumshypothese (Dawson 1999, S. 205)
- Hensel, Kurt. Nach Reichardt in Pieper, Hans (1974, S. 199). Zahlen aus Primzahlen. Berlin: DVdWiss.: "... zumal er auch noch mit seinen p-adischen Zahlen Transzendenzbeweise für e und kompliziertere Zahlen erbrachte, die nun wirklich falsch waren.".
- Hilbert. Existenzbeweise als "Theologie", so Paul Gordan über einen Beweis Hilberts.
- Hilbert. Frege kritisiert Hilberts Vermischung von Definition, Satz und Axiom (Brief an Heinrich Liebmann 29.7.1999)
- König, J.. Fehler im Beweis zur Widerlegung der Kontinuumshypothese von König bei seinem berühmten Vortrag 1904.
- Lamé. Liouville entdeckt Fehler im 'Beweis' zum großen Fermatschen Satzes von Lamé (1847).
- Lebesgue: In Hausdorffs Studien zur Dimensionstheorie hrsg. von H. Herrlich, M. Husek, G. Preufi ( S. 845) wird ausgeführt. " Erste Zusammenhänge zwischen Dimension und Überdeckungen sind bei H. LEBESGUE ([Leb 1911]) zu finden, wobei allerdings nur Teilmengen des |Rn betrachtet werden. Auch hatte LEBESGUES Arbeit zum Ziel, die Invarianz der Dimension (s. I)) zu beweisen, was jedoch zunächst nicht gelang, da der Beweis einen Fehler enthielt, worauf BROUWER in [Bro 1913] hinwies, und der erst zehn Jahre später von LEBESGUE in [Leb 1921] behoben wurde."
- Leibniz. Frege ("Grundzüge d. Arithmetik", S. 17: "Leibnizens Beweis von 2+2=4 hat eine Lücke".
- Lindemann. Fraenkel [äußert] sich ziemlich abfällig über Lindemanns - dem immerhin einer der großen (Beweise) in der Mathematikgeschichte gelang - Beweiskunst: "Bekannt wurde er durch seine wiederholten, in Aufsätzen und einer Monographie niedergelegten, ausnahmslos fehlerhaften Versuche, den 'Letzten Fermatischen Satz' zu beweisen."
- Neumann, C.G. (1870) Beweislücke (nach Schlote; 1887 geschlossen).
- Neumann, John von (1932). "1964 zeigte John Bell wo die Beweise von von Neumann, Gleason und Jauch und Piron fehlerhaft waren. Das Manuskript erschien allerdings erst 2 Jahre später (J. Bell, 'On the problem of hidden variables in quantum mechanics', Rev. Mod. Phys. 38 , 447 (1966).). Er entwickelte auch gleich ein Modell verborgener Variablen für einen Spin 1/2 (J.S. Bell, 'On the Einstein Podolsky Rosen paradox', Physics 1 , 195-200 (1964).). Das Ziel eines solchen Modells besteht darin, für eine beliebige Richtung des Analysators das Resultat der Messung mit Bestimmtheit vorauszusagen, wobei das Teilchen durch seinen Zustandsvektor Y und zusätzliche verborgene Variablen beschrieben wird." [D. Suter WS 1998/99 PDF 404]
- Poincarés preisgekroente Arbeit (die einen "Oskar" - Name des Königs von Schweden - brachte), die er 1989 eingereicht hatte, enthielt einen schweren Beweisfehler, der ihm erst bei der Überarbeitung so richtig deutlich wurde. Dieser Fehler war von den Jury (Mittag-Leffler, Hermité, Weierstraß) nicht bemerkt und erst bei den Druckvorbereitungen für die Acta mathematica einem Assistenten Mittag-Lefflers, Phragmén, aufgefallen. Die Vorauslieferungen wurden zurückgeholt und die Auflage eingestampft. Poincaré fand schließlich die Fehler und konnte ein Jahre die später die ganze Welt mit seiner Arbeit, die den Satz der Wiederkehr enthielt, Chaostheorie und Schmetterlingseffekt begründete, beeindrucken. Die peinliche Angelegenheit konnte bis Wissenschaftshistoriker den Nachlass von Mittag-Leffler durchforsteten und die Originalarbeit zum Vergleich gefunden wurde, vertuscht werden. Positiv sollte man nicht übersehen, dass gründliche Lücken- und Fehleranalyse großartige Resultate hervorbringen kann. Ausführliche Quelle: Szpiro, George G. (2009) Das Poincaré-Abenteuer. In (83-104) Denkanstöße 2009. Ein Lesebuch aus Philosophie, Kultur und Wissenschaft. München: Piper.
- Ruffinis Lücke durch Abel (1824) geschlossen: "Er hat seine Gründe dafür nie erklärt, und man mag sich fragen, was ihn dazu bewogen hatte. 1824, zwei Jahre nach Ruffinis Tod, veröffentlichte Abel seinen ersten Beweis der Unauflösbarkeit der Gleichung fünften Grades, der in vielen Belangen sehr nahe an Ruffinis Beweis liegt, allerdings eine wichtige Lücke schließt, die Ruffini nicht bemerkte. 1826 fiel Abel dann eine Zusammenfassung von Ruffinis Arbeiten in die Hände, und in seinem letzten, posthum veröffentlichten Artikel, erkennt Abel Ruffinis Leistung an: "Der erste und, falls ich mich nicht irre, einzige, der vor mir versucht hat, die Unmöglichkeit einer algebraischen Auflösung der allgemeinen Gleichung zu zeigen, ist der Geometer Ruffini. Doch sein Artikel ist so kompliziert, daß es sehr schwierig zu entscheiden ist, ob seine Schlußweise korrekt ist oder nicht. Mir scheint es, als sei seine Beweisführung nicht immer befriedigend.“ [Nach Sekundärquelle Pesic (2005, S. 88)].
- Russell: "Ich glaubte, daß Gewißheit in der Mathematik eher zu finden ist als anderswo. Doch ich entdeckte, daß viele mathematische Beweisführungen, welche meine Lehrer mir beibringen wollten, voller Trugschlüsse waren ..." Anmerkung: Church glaubte, so Guerrerio (2002, S. 62), daß sich in den PM von Whitehead & Russel mehrere Widersprüche und Fehler verbergen. Von Russell gibt es noch eine andere und merkwürdige Generalkritik an der Mathematik: "Die Mathematik ist die Wissenschaft, bei der man nicht weiß, wovon sie redet, noch ob richtig ist, was man sagt." [Quelle: The international Monthly, vol 4 (1901), p. 84]
- Steinersche Beweis Hilbert (1988) berichtet u.a. in Irrtümer in der Mathematik (S. 34-45; S. 37): "Lange ist der Steinersche Beweis für korrekt gehalten worden, da seine Methode viel von Dirichlet und Riemann angewandt wurde. Die Aufdeckung dieses grundlegenden Irrtums ist das Verdienst von Weierstrass." Anmerkung: Hilbert entwickelt in dieser Vorlesung auch eine psychologisch und wissenschaftssoziologisch interessante Fehlertheorie.
- Tschebyschow 1887. Beweislücken beim Zentralen Grenzwertsatz, verbessert Markow 1898, vollständig Ljapunow 1901.
- Perelemans Beweis der Poincaré Vermutung. Novost vom 25.8.6 [Q] führt aus: "Es liegt mir fern, das Mathematikermilieu zu idealisieren. Dort werden vielleicht noch schlauere Intrigen gesponnen als um die Ballerina Anastassija Wolotschkowa im Bolschoi-Theater. Als Grigori Perelman 2002 seinen ersten Beitrag zum Problem der Poincaré-Vermutung veröffentlichte, zweifelte er bestimmt auch selbst an der Richtigkeit seiner Beweise. Ein Genie zweifelt immer, eine Mittelmäßigkeit nie. Und vier lange, qualvolle Jahre wartete er auf das Wichtigste: die Anerkennung der Richtigkeit seiner Beweise. Wie wir sehen, hatten es seine Kollegen beziehungsweise Opponenten nicht eilig. Die Entscheidung unterschrieben drei führende Mathematiker der Welt: Tien, Kleiner und Lott. Die Formulierung zeugt davon, dass sie sich und ihrem wissenschaftlichen Ruf absolut nichts vergeben haben. Sinngemäß heißt es darin: Trotz einiger geringfügiger Ungenauigkeiten und selbst kleiner Fehler sind Perelmans Beweise korrekt."
Hinzu kommt der bis heute nicht ausgestandene Grundlagenstreit
und viele, viele Verständnis- und Bedeutungsprobleme ([Korrelation],
[Signifikanz-Statistik]) in der
Schule und Anwendung. Seit [Cantors]
Höllenparadies, der [Meschuggeisierung
des Zählens] und der Mathematisierung
der "Welt" - in den Sozialwissenschaften mit meist nicht erfüllten
Voraussetzungen - scheint die Mathematik ihren großen Nimbus absoluter
Sicherheit und Zuverlässigkeit zunehmend einzubüßen. Die
Kluft zwischen Theorie und nicht- naturwissenschaftlich- technischer Praxis
wird immer größer.
Exkurs V: Mehr oder minder gut beweisen ?
Des öfteren kennzeichnen MathematikerInnen einen Beweis als "streng". Daraus folgt unmittelbar, dass es offenbar unterschiedlich strenge Beweise gibt. Gelegentlich wird eine "Beweisidee" geäußert. Ähnlich ist wohl die Formulierung "Beweisandeutung" einzuschätzen. Mehr Information wird gegeben, wenn eine "Beweisskizze" ausgeführt und damit ein Weg gewiesen wird. Man liest auch zu weilen von einem "vollständigen" Beweis, woraus sich sofort ergibt, dass es wohl auch mehr oder minder unvollständige gibt. Und es gibt die "Beweislücke", wenn etwas fehlt, sei sie schließbar oder auch nicht. Eine echte, mit den jeweils aktuell zur verfügung stehenden Mitteln nicht schließbare Beweislücke ist ein "Beweisfehler", wovon man wohl eine ganze Reihe unterschiedlicher unterscheiden kann. All das wird den SchülerInnen im Mathematikunterricht nicht beigebracht, wie es überhaupt an einer wirklich durchdachten und differenzierten Beweislehre zu fehlen scheint. Beweisen wird vorgemacht, gezeigt, nach gemacht und geübt, aber nicht richtig gelehrt, vermutlich nicht einmal an der Universität. Fragen sind unerwünscht, geschweige denn Kritik, wie Lakatos (S. 134) ebenso ernüchternd wie geißelnd klar auf den Punkt bringt:
"Die Euklidische Methodenlehre hat einen gewissen verbindlichen Darstellungsstil entwickelt. Ich werde ihn den ,deduktivistischen Stil' nennen. Dieser Stil beginnt mit einer sorgfältig zusammengestellten Liste von Axiomen, Hilfssätzen und/ oder Definitionen. Die Axiome und Definitionen erscheinen häufig gekünstelt und geheimnisvoll verwickelt. Niemals wird mitgeteilt, wie diese Verwicklungen zustandekamen. Der Liste der Axiome und Definitionen folgen in sorgfältiger Wortwahl die Sätze. Diese sind beladen mit umständlichen Bedingungen; es erscheint unmöglich, daß irgendjemand sie jemals erraten hat. Dem Satz folgt der Beweis.
Der Mathematikstudent ist nach dem Euklidischen Ritual dazu verpflichtet, dieser Darbietung eines Zauberkunststückes beizuwohnen, ohne eine Frage zu stellen, sei es zum Hintergrund, sei es zur Durchführung einer kleinen Nebenüberlegung. Falls der Student zufällig entdeckt, daß einige dieser ungefügen Definitionen beweiserzeugt sind, falls er sich einfach wundert, wie diese Definitionen, Hilfssätze und der Satz eigentlich dem Beweis vorangehen können, dann wird ihn der Zauberer wegen dieser Zur-Schau-Stellung seiner mathematischen Unreife ächten [FN255].
[FN255: Einige Lehrbücher behaupten, daß sie beim Leser keinerlei Vorkenntnisse voraussetzen, sondern lediglich eine gewisse mathematische Reife. Das bedeutet häufig, daß sie vom Leser erwarten, daß ihn die Natur mit der .Fähigkeit' ausgestattet hat, einen Euklidischen Beweisgang ohne ein unnatürliches Interesse am Problemzusammenhang, an der Heuristik des Beweisganges hinzunehmen.] " [siehe bitte auch]
Gerne werden Beweise oder Beweisteile dem Leser "überlassen",
nicht selten wird auch verzichtet durch Formulierungen, "wie man leicht
sieht" oder "wovon sich der Leser leicht überzeugen kann" oder es
wird suggeriert, das sich eine Folgerung "sofort" ergibt. Besonders "motivierend"
sind auch Hinweise, dass sich weitere Ausführungen erübrigen,
weil ein Sachverhalt angeblich "trivial" sei, anscheinend ist "Trivialität"
ein großes Übel, das nur ganz schwer überwunden werden
kann. Die eigene Bequemlichkeit, manchmal vielleicht sogar Unvermögen
wird auch gerne pädagogisch kaschiert, indem dem Leser mitgeteilt
wird, dass er zur Übung dieses oder jenes selbst beweisen solle.
Literatur Beweis und beweisen in Mathematik und Logistik(Auswahl)
Siehe bitte auch Geschichte des Grundlagenstreits in der Mathematik und Literaturliste Beweis und beweisen in Logik, Erkenntnis-, Wissenschaftstheorie und Philosophie.
- Ackermann, Wilhelm (1925) Begründung des ,,tertium non datur" mittels der Hilbertschen Theorie der Widerspruchsfreiheit. Mathematische Annalen / Zeitschriftenband (1925) / Artikel / 1 - 36:
- Aigner, Martin & Ziegler, Günther M. (2002) Das BUCH der Beweise.
- Barrow, John, D. (dt. 1999, engl. 1992). Ein Himmel voller Zahlen. Auf den Spuren mathematischer Wahrheit. Reinbek: Rowohlt.
- Behnke, H.; Remmert, R.; Steiner, H-G. & Tietz, H. (1964) Das Fischer Lexikon Mathematik 1. Frankfurt Fischer.
- Behnke, H.; Tietz, H. (1966, Hrsg.) Das Fischer Lexikon Mathematik 2. Frankfurt Fischer.
- Boutroux, P. (1927). Das Wissenschaftsideal der Mathematiker. XXVIII. Bd. Wissenschaft und Hypothese. Leipzig: Teubner.
- Brouwer, L.E.J. (1924). Über die Bedeutung des Satzes vom ausgeschlossenen Dritten in der Mathematik, insbesondere in der Funktionentheorie. Journal für die reine und angewandte Mathematik, Bd. 154, 1, 1-7. Siehe auch Heyting.
- Dalen, Dirk, van (1992, Hrsg.). L.E.J. Brouwer. Intuitionismus. Mannheim: B.I. [darin ein Werkverzeichnis]
- Euklid > Link; siehe auch Heyting.
- Davis, Philip. J. & Hers, Reuben (dt. 2.k. A. 1996, engl. 1981). Erfahrung Mathematik. Basel: Birkhäuser.
- Dudley, Underwood (dt. 1995). Mathematik zwischen Wahn und Witz. Basel: Birkhäuser.
- Enriques, F. (1927). Zur Geschichte der Logik. Grundlagen und Aufbau der Wissenschaft im Urteil mathematischer Denker. XXVI. Bd. Wissenschaft und Hypothese. Leipzig: Teubner.
- Esser, Wilhelm Karl (1964). Aufzählbarkeit und Cantorsches Diagonalverfahren. Untersuchungen zu Grundfragen der Logik. Dissertation, Philosophische Fakultät LMU München.
- Felgner, Ulrich (2012) Das Induktions-Prinzip. Jahresber Dtsch Math-Ver (2012) 114:23–45.
- Freund, H. & Sorger, P. (1974). Aussagenlogik und Beweisverfahren. Mathematik für die Lehrerausbildung. Stuttgart: Teubner.
- Freund, H. & Sorger, P. (1976). Logik, Mengen, Relationen. Praxis des mathematischen Beweisens. Mathematik für die Lehrerausbildung. Stuttgart: Teubner.
- Frey, Gerhard (1967) Die Mathematisierung der Welt. Stuttgartd: Kohlhammer.
- Friedman, Harvey (1975). One Hundred And Two Problems In Mathematical Logic. The Journal of Symbolic Logic Vol. 40, 2, 113-129.
- Hilbert, D. & Ackermann, W. (4.A. 1959). Grundzüge der theoretischen Logik. Berlin: Springer.
- Hilbert, D. nach Ackermann, W. (1988). Wissen und mathematisches Denken. Vorlesung von Prof. D. Hilbert W.S. 1922/23. Ausgearbeitet von W. Ackermann. Mathematisches Institut Universität Göttingen.
- Heyting, A. (1930). Die formalen Regeln der intuitionistischen Logik. Sitzungsberichte der preußischen Akademie der Wissenschaften, Physikalisch-Mathematische Klasse. Berlin: De Gruyter.
- Heyting, A. (1975, Ed.). L.E.J. Brouwer. Collected Works 1. Philosophy and Foundations of Mathematics. Amsterdam: North-Holland.
- Hilbert, D. (1931) Beweis des Tertium non datur. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-... (1895) / PeriodicalVolume 1931 (1931),
- Kondakow, N.I. (dt. 1978 russ. 1975). Wörterbuch der Logik. Berlin: deb.
- Lakatos, Imre (dt. 1979, engl. 1976). Beweise und Widerlegungen. Die Logik mathematischer Entdeckungen. Braunschweig: Vieweg.
- Lakatos, Imre (dt. 1982, engl. 1978). Mathematik, empirische Wissenschaft und Erkenntnistheorie. Philosophische Schriften Band 2. Herausgegeben vpn John Worrall & Gregory Currie. Braunschweig: Vieweg.
- Lecat, Maurice (1935). Erreurs de Mathématiciens des origines à nos jours. Bruxelles: Librairie Casteigne. [Eine Bibliographie mathematischer Fehler mit mehreren Index-Verzeichnissen: Liste der Periodika mit den fehlerhaften Arbeiten; Liste der Periodika mit den Fehlerkorrekturen; Jahresangabe in der die Fehler produziert wurden; Jahresangaben in denen die Fehler korrigiert wurden; Liste der Fehlerautoren; Liste der Fehler Korrigierer]
- Lietzmann, W. (1950). Wo steckt der Fehler? Mathematische Trugschlüsse und Warnzeichen. Leipzig: Teubner.
- Lorenzen, Paul (1962). Meta-Mathematik. Mannheim: B.I.
- Mason, John; Burton, Leone & Stacey, Kaye (dt. 1988, engl. 1982). Hexeneinmaleins: kreativ mathematisch denken. München: Oldenbourg.
- Meinel, Christoph & Mundhenk, Martin (2009). Mathematisches Beweisen. In (58-63): Mathematische Grundlagen der Informatik. Wiesbaden: Vieweg+Teubner.
- Meschkowski, Herbert (1976). Richtigkeit und Wahrheit in der Mathematik. Mannheim: B.I.
- Pesic, Peter (2005). Abels Beweis. Berlin: Springer. ISBN: 9783540222859 [I]
- Pieper, Herbert (1984). Die komplexen Zahlen. Theorie, Praxis, Geschichte. Berlin: VEB d.W.
- Poincaré (1914) Wissenschaft und Methode. Autorisierte deutsche Ausgabe mit erläuternden Anmerkungen von F. und L. Lindemann. Leipzig und Berlin: Teubner.
- Poincaré, Henri (1914). Wissenschaft und Hypothese. Autorisierte deutsche Ausgabe mit erläuternden Anmerkungen von F. und L. Lindemann. Dritte verbesserte Auflage. Leipzig und Berlin: Teubner.
- Polya, Georg (dt. 1949, engl.?). Schule des Denkens. Vom Lösen mathematischer Probleme. [mit: "Teil III. Kleines Wörterbuch der Heuristik] Bern: Francke.
- Polya, Georg (dt. 1962-63, engl. 1954 ). Mathematik und plausibles Schließen. Bd. I Induktion und Analogie in der Mathematik. Bd. II. Typen und Strukturen plausibler Folgerung. Basel: Birkhäuser.
- Potthoff, Klaus (1981). Einführung in die Modelltheorie und ihre Anwendungen. Darmstadt: WBG.
- Prestel, Alexander (1986). Einführung in die Mathematische Logik und Modelltheorie. Braunschweig: Vieweg.
- Rademacher,H. & Toeplitz, O. (1930, Nachdruck 1968). Von Zahlen und Figuren. Proben mathematischen Denkens für Liebhaber der Mathematik. Berlin: Springer.
- Ruzsa, Imre (1976) Die Begriffswelt der Mathematik. Berlin: Volk und Wissen.
- Schütte, Kurt (1960). Beweistheorie. Berlin: Springer.
- Schwarz, Walter (1975). Brücke zur Höheren Mathematik. Einführung in Methode und Technik. Reinbek: Rowohlt-Vieweg.
- Sinowjew, A.A. (dt. 1968, russ. 1968). Über mehrwertige Logik. Ein Abriß. Braunschweig: Vieweg.
- Tarski, Alfred: Internet-Quellen (nach H.Kremer).
- Thiele, Rüdiger (1979). Mathematische Beweise. Leipzig: Teubner.
- Whitehead, N. & Russell, B. (1910-1913). Principia Mathematica. [,1,2,3,]
- Wittenberg, Alexander (1957) Vom Denken in Begriffe, Mathematik als ERxperiment des reinen Denkens. Basel: Birkhäuser.
- Zahn, Peter (1979). Beweisen im Mathematik-Unterricht. Didaktische Anwendungen. Die Lehre vom logischen Schließen. Darmstadt: Wissenschaftliche Buchgesellschaft.
_
Links Beweis und beweisen in Mathematik und Logistik (Auswahl)
Geänderte URLs ohne Weiterleitung entfernt (10).
- Allgemeine Mathematik-Internet-Quellen: hier.
- Euklid: http://aleph0.clarku.edu/~djoyce/java/elements/Euclid.html.
- Allgemein mit vielen Hinweisen und Links: http://www.mathematik.de/.
- Beweis (Mathematik): http://de.wikipedia.org/wiki/Beweis_(Mathematik).
- Beweisen im Mathematikunterricht: Zum Begründungsverständnis von Abiturientinnen und Abiturienten: http://www.math.uni-oldenburg.de/didaktik/beweisen/.
- Beweis des Mittelwertsatzes: http://home.arcor.de/enibuddy/mathe/mittel1.htm.
- Wann ist ein Beweis ein Beweis? Von ERICH CHRISTIAN WITTMANN und GERHARD MÜLLER, Dortmund: Der indirekte Beweis: didmath uni-erlangen Material indbew.
- matheplanet: http://www.matheplanet.com/matheplanet/.
- Beweis zur Summen-Score-Funktion (Rührig, Wiesent).
Glossar, Anmerkungen, Endnoten: > Eigener wissenschaftlicher Standort.
GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
__
abfällig. Als ich den abfälligen Absatz Fraenkels über Lindemann [W] das erste mal las, wunderte ich mich und fand diese Entwertung merkwürdig und unangemessen. Später las ich, dass Lindemann und seine Frau Poincaré, einer der schärfsten Kritiker Cantors, der Mengenlehre und neuen Logik (Logistik), übersetzten. Aha, dachte ich, daher könnte also der Wind wehen.
Fraenkel über von Lindemanns Beweiskunst

___
Aber: Grundlagenstreit John
D. Barrow teilt in seinem interessanten Buch mit (S. 344f): "Im Westen
sorgte Errett Bishops Arbeit mit dem Titel Foundations of Constructive
Analysis 1967 für ein erneutes Interesse an der konstruktiven
Mathematik. Die Gründe sind interessant. Erstens war Bishop ein angesehener
Mathematiker, der in der Mathematik mit herkömmlichen Beweismethoden
gearbeitet hatte. Er stellte seine Ideen in einer klaren und lesbaren Form
dar, die [<344} jeder Berufsmathematiker verstehen konnte. Zweitens
strafte sein Buch die Behauptung Lüge, daß der Konstruktivismus
die Mathematik vieler der ihr liebsten Güter berauben würde.
Bishop zeigte, daß sich ein sehr großer Teil der herkömmlichen
Mathematik dem Fundus konstruktivistischer Wahrheiten hinzufügen ließ,
wenn man nur einfallsreich genug war. Drittens war Bishops Werk Mathematik
und nichts als Mathematik. All die philosophischen und mystischen Elemente
aus Brouwers System waren darin nicht mehr enthalten, und außerdem
war Bishop zweifellos ein sympathischer Mensch. Bishop entwickelte den
konstruktiven Ansatz nachgerade in der Absicht, unbeweisbare philosophische
Überlegungen aus der Mathematik herauszuhalten. In der Einführung
zu seinem Buch macht er die berühmte Bemerkung: 'Die Mathematik gehört
zu den Menschen, nicht zu Gott. Wir sind nicht an den Eigenschaften der
positiven Zahlen interessiert, die für den endlichen Menschen keine
deskriptive Bedeutung haben. Wenn ein Mensch beweist, daß eine positive
ganze Zahl existiert, sollte er wissen, wie er sie finden kann. Wenn Gott
seine eigene Mathematik hat, die getan werden muß, soll er es selber
tun.' Der letzte und interessanteste mögliche Grund für die Resonanz
von Bishops Buch ist, daß es zu einer Zeit erschien, als sich der
Computer für Mathematiker und Wissenschaftler zu einem wichtigen Instrument
entwickelte. Man erlebte, wie Rechner große und schwierige Probleme
lösten, indem sie eine endliche Folge deduktiver Schritte für
Eingaben ausführten, die ausschließlich aus Zahlen bestanden.
Diese Neuerungen hinterließen ihre Spuren bei Bishop, der daraufhin
die Mathematik als eine «gehobene Programmiersprache sah, in der
sich Beweise abfassen ließen. Mit Existenzbeweisen sollten dann ganz
natürlich Algorithmen einhergehen.» Bishop glaubte, mathematische
Objekte seien in dem Sinn völlig objektiv, daß jeder mathematische
Satz sich in eine verifizierbare oder berechenbare Aussage über Zahlen
übersetzen läßt. Wenn alle Konstruktionen von Hand ausgeführt
werden [<345] müßten, könnte sich die praktische Durchführbarkeit
als entscheidendes Hindernis erweisen, aber die Aussicht auf rasche elektronische
Durchführung der Schritte enthebt uns dieser Sorge. Zumindest veränderte
sich die Einstellung der Mathematiker hier wesentlich. Als immer mehr Mathematiker
begannen, Computer zu verwenden, übernahmen sie damit auch unbewußt
die Auffassung, daß mathematische Existenz «berechenbare Existenz»
beinhaltet. Bishop versuchte also, Mathematiker in eine Richtung zu drängen,
in die die Welle des technischen Fortschritts sie ohnehin schon spülte.
Brouwer dagegen hatte versucht, gegen den Strom zu schwimmen. In der Zeit
vor dem Krieg konzentrierte sich die Mathematik auf die erfolgreichen Schöpfungen
Mengentheorie, transfinite Zahlentheorie und Logik, die ihrem Wesen nach
alle nicht konstruktiv waren. [FN Ich habe mich oft gefragt, was Brouwer
mit den Entdeckungen von Turing und anderen zur Berechenbarkeit angefangen
hat, aber meine Suche in Brouwers Arbeiten und Biographien haben keinerlei
Hinweise auf irgendwelche persönlichen Begegnungen oder einen Gedankenaustausch
ergeben.] Man ist versucht zu sagen, daß Bishop zeitgemäß
war, aber natürlich «wählte» Bishop nicht etwa die
günstigste Zeit. Bishop wurde durch das Aufkommen der algorithmischen
Denkweise beeinflußt, und dies, so könnte man vermuten, führte
ihn dazu, sich auf die neue Bedeutung konstruktiver Methoden zu konzentrieren."
Ausführlich zum Grundlagenstreit
in der Mathematik.
___
Cranz
schreibt noch 1895 (S. 20) Paul du Bois-Reymond zitierend: "Noch heute
erscheinen in der 'unfehlbarsten aller Wissenschaften' kaum zwei Lehrbücher
hinter einander, die, wenn sie auf die Grundbegriffe näher eingehen,
nicht auf das Schroffste sich widersprächen."
___
Dawson,
John W. (1999). Das logische Dilemma. Leben und Werk von Kurt Gödel.
Berlin: Springer.
___
Fehlertheorie Hilberts (1922/23)
bei Fehlschlüssen in der Mathematik: "Bevor ich weitere Beispiele
behandele, möchte ich Ihnen ein wenig zu erklären versuchen,
wie solche Irrtümer zustande kommen und worin dann ihre allgemeine
Bedeutung besteht. Es hat damit folgende Bewandtnis: Allemal wenn eine
neue fruchtbare Methode ersonnen wird zur Lösung von Problemen, zur
Erweiterung unseres Wissens, zur Eroberung neuer Provinzen der Wissenschaft,
gibt es einerseits kritische Forscher, die der Neuerung gegenüber
mißtrauisch sind und andererseits solche, die an Kühnheit es
allen zuvortun, die noch unerschöpfte und ergiebige Quellen gründlich
ausnutzen, rasch Neues finden und daher bald das Übergewicht bekommen,
sodaß die Einwendungen der Kritiker verstummen. Dies ist die Periode
des raschen Fortschreitens der Wissenschaft. Oft sind es gerade die besten
Pioniere, die sich am weitesten vorwagen und dann auch am ehesten auf unsicheres
Terrain kommen. Anzeichen für den letzteren Fall sind Unklarheiten
und Zweifelhaftigkeiten der erhaltenen Resultate, bis sich schließlich
offenbare Widersprüche und Widersinnigkeiten, sogenannte Paradoxien,
herausstellen. In diesem Augenblick erscheinen nun die kritisch Gesonnenen,
die bisher beiseite standen, wieder auf dem Plan, bemächtigen sich
der Paradoxien, decken wirkliche Irrtümer auf und versuchen nun ihrerseits
die ganze Methode zu verdächtigen und zu verwerfen. Es besteht dann
die Gefahr, daß alles Errungene wieder verloren geht. Es ist dann
immer die wichtigste Aufgabe, diese über das Ziel gehende Kritik einzudämmen
und eine Neubegründung der Methode zu versuchen, sodaß sie vor
jeder falschen Anwendung gesichert ist und die gewonnenen Resultate in
den festen Bestand der mathematischen Erkenntnis eingereiht werden können."
In Hilbert n. Ackermann
(1988, 38f)
___
Gordan, Paul. "Aber gerade weil
der Hilbertsche Beweis ziemlich einfach war, stiess er zunächst auf
Unverständnis und Ablehnung unter den Mathematikern. Denn es handelt
sich um einen reinen Existenzbeweis, der bei gegebenem Ideal A kein effektives
Verfahren zur Konstruktion der endlich vielen Erzeugenden von A angibt.
Die Mathematiker der damaligen Zeit waren an Existenzbeweise dieser Art
nicht gewöhnt, jedenfalls nicht in der Algebra. Gordan selbst kritisierte:
“Das ist keine Mathematik, das ist Theologie”.
Wobei er mit “Theologie” meinte, bei einem solchen Beweis müsse
man wie in der Religionswissenschaft an die Richtigkeit der Schlussweisen
glauben. Das widerspricht jedoch den Grundsätzen der Mathematik, denn
alle mathematischen Beweise müssen doch durch logisches Denken nachprüfbar
sein, ohne an einen “Glauben” zu appellieren! Heute akzeptiert man in der
Algebra auch reine Existenzbeweise, nicht zuletzt unter dem Einfluss der
Cantorschen Mengenlehre. Übrigens hat Hilbert in einer weiteren Arbeit
seinen Beweis tatsächlich ergänzt durch eine effektive Abschätzung
der Grade der Polynome, die das gegebene Ideal A erzeugen – und er hat
damit auch Gordan von der Richtigkeit seiner Beweisführung überzeugen
können."
Online-Quelle (S.12): Peter Roquette, Mathematisches
Institut, Universität Heidelberg, Vortrag "David Hilbert
in Königsberg" am 30.9.2002 an der Mathematischen Fakultät
in Kaliningrad 17. September 2002
___
Guerrerio, Gianbruno (2002). Kurt Gödel.
Logische Paradoxien und mathematische Wahrheit. Spektrum der Wissenschaft,
Biografie,1.
___
Hilbert, David (1904). Über
die Grundlagen der Logik und der Arithmetik. Verhandlungen des III. internat.
Mathematiker Kongresses in Heidelberg 1904, abgedruckt als Anhang zur 3.
Auflage von Hilberts Grundlagen der Geometrie.
___
Körperaxiome. In der Mathematik
und Zahlentheorie gibt es ganz verschiedene Zahlen.
Man könnte alltagssprachlich auch von unterschiedlichen Zahlen-Typen
sprechen. Die verschiedenen Zahlentypen können durch unterschiedliche,
sog. Körper-Axiome definiert werden. In einem Zahlenkörper (K2)
z.B., in dem es nur die beiden Zahlen 1 und 0 gibt, ergeben sich von der
Alltagserwartung überraschende und abweichende Ergebnisse bei den
arithmetischen Operationen, nämlich 1+1=0.
___
Logistik. "Logistik" bezeichnet mindestens
ein dreifaches Homonym [1,
2,
3,
4,
5,
].
(1) Logistica (rechnen) hieß einst die praktische
Rechenkunst auf lateinisch.
(2) Nach Mittelstraß
(1984, S. 703) wurde der Ausdruck Logistik auf dem 2. Philosophenkongress
in Genf 1904 von Couturat, Lalande und Itelson als Bezeichnung für
die kalkülisiert auftretende formale Logik zum Zwecke der terminologischen
Abgrenzung von der traditionellen Logik vorgeschlagen worden. Danach wurden
die mathematischen Logiker etwa bis in die 70 er Jahre mit ihrer strengen
Formelsprache auch Logistiker genannt (Beispiele: Becker, Oskar (1951).
Einführung in die Logistik. Bochenski, Joseph M. (1954). Grundriß
der Logistik. Dürr, Karl (1954). Lehrbuch der Logistik, Johann Fischl
(1967). Logik. Ein Lehrbuch mit einem kurzen Abriß über Logistik.
Jacoby, Günther (1962). Die Ansprüche der Logistiker auf die
Logik und ihre Geschichtsschreibung. Bruno von Freytag gen. Löringhoff
(1961). Logik. Ihr System und ihr Verhältnis zur Logistik). Die "rein"
mathematischen Logiker selbst benutzen diesen Ausdruck gewöhnlich
nicht. Nachdem die Logik weitgehend von den MathematikerInnen angeeignet
wurde, hat sich ihre Ausdrucksweise durchgesetzt und der Ausdruck "Logistik"
ist zunehmend in den "logik-öffentlichen" Hintergrund getreten. Am
besten übersetzt man sich Logistik in diesem Sinne mit streng kalkülisierter
Logik. Mathematische Logik trifft es aber auch sehr gut. Tatsächlich
hat "...istik" für manche doch eine negative Tönung, was von
einigen philosophischen WortverwenderInnen so beabsichtigt sein konnte.
Was an mathematischer Logik aber negativ sein sollte, ist zunächst
nicht zu verstehen, außer daß, was MathematikerInnen unter
ihre Fittiche nehmen, sehr schnell allgemein sehr unverständlich wird
(so Goethe in einem
Brief am 17.5.1829 an Zelter "Die Mathematiker sind eine Art Franzosen:
redet man zu ihnen, so übersetzen sie es in ihre Sprache, und dann
ist es alsbald ganz etwas Anderes.")
(3) Die dritte Bedeutung betrifft das Gebiet der
Planung und Organisation, hat damit aber auch Berührungspunkte zur
Mathematik, am meisten vielleicht zu dem Gebiet der Optimierung (z.B. Transport,
Lagerhaltung) und der praktisch angewandten Spieltheorie. Einfacher könnte
man von Planung, Strategie und Taktik sprechen. Diese Anwendungen spielen
eine große Rolle in der Wirtschaft (dort heißt ein Teilfachgebiet
sogar "Logistik"); aber auch im Militär- und Kriegswesen, im
Sport und ganz allgemein im Leben.
__
Mathematik. Mathematik verstehe ich
als die formale Wissenschaft von idealen Objekten und Beziehungen, in der
alle mögliche (Modell) [Welten] konstruierbar
sind, die auf reale Weltprobleme angewendet (angewandte M.) werden können
oder nicht (reine M.). Sog. reine Mathematik interessiert sich nicht für
Anwendungsfragen und muß das natürlich auch nicht, so wie reine
Psychologie sich nicht darum zu kümmern braucht, ob und wie reine
Psychologie angewandt werden kann. In der Psychologie gibt es allerdings
eine natürliche Schnittstelle zur Anwendung: man kann über die
Psyche der Menschen nichts erforschen, wenn man nicht mit den Menschen
interagieren und kommunizieren kann. Eine reine MathematikerIn braucht
im Prinzip keine andere und könnte auch ganz alleine für sich
reine Mathematik betreiben; Ramanujan
war womöglich längere Zeit so einer. Es mag davon sogar viele
geben, aber davon können wir nichts wissen: eine neue Paradoxie ;-)?
__
Mathematikkritik
Schopenhauer kritisierte den sog. (Euklid'schen) Mausefallenbeweis.
Quellen: S. 55: Schopenhauer, Arthur (1847) Ueber die vierfache Wurzel
des Satzes vom zureichenden Grunde. Eine philosophische Abhandlung. [PDF
bei Wikimedia.org]
__
mit wenigen Ausnahmen. Barrow
(S. 283-288) berichtet die Geschichte von Ramanujan, von Rao entdeckt
und Hardy gefördert, einem offenbar genialen und leidenschaftlichen
indischen Ausnahme-Mathematiker, der nur 33 wurde, aber die ganze Mathematikerwelt
mit seinen Formeln in Aufregung versetzte, wobei er nach Hardy offenbar
nie das übliche Beweisen lernte oder sich aneignete und mit einer
Mischung aus Intuition - im üblichen Sinne - und Induktion (Beispiele
und probieren) arbeitete, doch so erfolgreich, daß die größte
Kapazität seiner Zeit einigen Ergebnissen nicht zu folgen vermochte.
Er soll der Inbegriff eines reinen Mathematikers gewesen sein, der sich
auch nie für Anwendungsfragen interessierte, sondern ausschließlich
für die Beziehungen seiner Zahlen.
___
Modelle (Meßtheorie). Als Hauptsatz
in der Meßtheorie könnte gelten: Zwischen dem mathematischen
und empirischen Meßmodell existiert eine homomorphe Abbildung, wobei
diese Homomorphie von der AnwenderIn für die jeweilige Anwendung zu
zeigen wäre. Allgemeinverständlich wird man fordern: die angewandte
Mathematik muß dem empirischen Gegenstandsbereich angemessen sein,
nicht zu weit und nicht zu eng, nicht zu viel und nicht zu wenig. Im allgemeinen
ist es so, daß die Mathematik in der sozialwissenschaftlichen und
besonders psychologischen Anwendung eine Genauigkeit vortäuscht, die
empirisch meist nicht begründet ist. Bereits eine Mittelwertbildung
setzt ein Skalenniveau voraus, das in aller Regel empirisch nicht begründet
und nicht gezeigt wurde. "Messen" in der Psychologie ist gewöhnlich
messen per fiat - Ausdruck von: Orth, B. (1974). Einführung
in die Theorie des Messens. Stuttgart: Kohlhammer, S. 41 unter Bezugnahme
auf Torgerson, Pfanzagl und Fischer - ein völlig unhaltbarer
Zustand für eine Wissenschaft.
___
petitito principii. Vorwegnahme
des Grundes. Es wird ein Beweismittel verwendet, das selbst
nicht bewiesen ist und selbst noch des Beweises bedarf. Auch der circulus
vitsiosus kann als Variante der p.p. angesehen werden, da der Zirkelschluß
sich selbst beim Beweis verwendet bzw. voraussetzt (ein kluger Kopf ist
intelligent; ein Kreis ist rund). Die indische Logik nennt diesen Fehler
siddha-sadhya, wenn der Beweis selber des Beweises bedarf, so das Wörterbuch
der Logik.
___
Russell. Zitiert nach (S. 350f): Davis,
Philip. J. & Hers, Reuben (dt. 2.k. A. 1996, engl. 1981). Erfahrung
Mathematik. Basel: Birkhäuser.
___
Voraussetzungen und Mittel
Zwar ist im allgemeinen Beweisschema der Schulmathematik die Angabe der
Voraussetzungen vorgesehen, aber nicht wie viel und wie weit zurück.
Nicht selten liest man, dass man zum Aufbau der Mengenlehre auf die Prädikatenlogik
1. Stufe zurückgreift. Andererseits stößt man in der Ausarbeitung
der Prädikatenlogik 1. Stufe auf Bezugnahmen zur Mengenlehre. Das
wirkt zumindest zirkulär. Was braucht man z.B. "alles", wenn man den
Satz des Pythagoras verwenden will? Oder, anders herum, was setzt man -
ohne sich im einzelnen darüber oft Rechenschaft abzulegen - bei diesem
oder jenen der vielen, vielen Beweise des Satzes des Pythagoras zu Recht
oder zu Unrecht voraus? Die Idee einer lückenlos logischen Vernetzung
und Begründung zeigt sich in der Notation von Wittgensteins tractatus,
der hiervon offenbar durch das Logizismus Programm der Mathematik wie es
Whitehead & Russel in der Principia mathematica (W)
durchführten, inspiriert wurde. Und es ist wahrscheinlich kein Zufall,
dass die französische Mathematikergruppe "Bourbaki" [W]
ab 1934 einen rigoros strengen Aufbau der Mathematik nach den Hilbert-Grundsätzen
durchführte.
__
Wittgenstein
und vollstaendige Induktion
Materialien:
Ramharter, Esther (2014) Wittgenstein über vollständige
Induktion Wittgenstein-Studien. Band 5, Heft 1, Seiten 179–204, ISSN (Online)
1868-7458, ISSN (Print) 1868-7431, March 2014.
Abstract In seiner mittleren Phase, insbesondere in Philosophischen
Bemerkungen und Philosophische Grammatik, widmet Wittgenstein längere
Passagen der vollständigen Induktion. Nach einer groben Skizze (1)
einiger grundsätzlicher Einstellungen und Erwägungen Wittgensteins
wird im vorliegenden Beitrag zunächst (2) versucht, seine Kommentare
aus jener Perspektive, die Mathematiker auf die Induktion und die Arithmetik
haben, einzuordnen und möglichst kompatibel damit zu interpretieren.
Nach einem kurzen Einschub (3) zur Bedeutung des Mathematikers Albert Thoralf
Skolem für Wittgenstein, soll (4) herausgearbeitet werden, inwiefern
Wittgenstein zur Induktion eine eigene, von der üblichen abweichende
Auffassung vertritt. In diesem vierten Abschnitt wird versucht, Induktion
und Arithmetik aus der Perspektive Wittgensteins zu beschreiben. Dabei
wird sich zeigen, dass sich eine Robinson-Arithmetik als formale Entsprechung
für Wittgensteins Standpunkt anbietet. Daran schließt (5) eine
Erörterung der Frage an, inwiefern er daher eine revisionistische
Position vertritt.
__
Geschichte des Grundlagenstreits in der Mathematik
Absurdität, Antinomie, Aporie, Konfusion, Paradoxie, Pseudo-Paradoxie, Sophisma, Widersprüche, X-Strittiges/Sonstiges.
Einführung, Überblick, Verteilerseite Beweis und beweisen
Überblick: Abstrakte Grundbegriffe aus den Wissenschaften
| IP-GIPT, z.B.
mit Hilfe von "google": <suchbegriff>
site: www.sgipt.org
z.B. Beweis beweisen site: www.sgipt.org * Logik site: www.sgipt.org |
Dienstleistungs-Info.
*
Sponsel, Rudolf (DAS). Beweis und beweisen in Mathematik und Logistik. Blicke über den Zaun zum Auftakt für eine psychologisch-psychotherapeutische Beweislehre. Abteilung Abstrakte Grundbegriffe aus den Wissenschaften: Analogien, Modelle und Metaphern für die allgemeine und integrative Psychologie und Psychotherapie sowie Grundkategorien zur Denk- und Entwicklungspsychologie. Internet Publikation - General and Integrative Psychotherapy IP-GIPT. Erlangen: https://www.sgipt.org/wisms/gb/beweis/b_mathe.htm
Copyright & Nutzungsrechte
Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das direkte, zugriffsaneignende Einbinden in fremde Seiten oder Rahmen ist nicht gestattet, Links und Zitate sind natürlich willkommen. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus ... geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.
korrigiert irs 30.8.3
Änderungen wird gelegentlich überarbeitet, ergänzt und vertieft * Anregungen und Kritik erwünscht
02.09.23 Dedekind Zitat genaue Quellenangabe.
04.08.18 Ergänzung Suggestivfrage in Gefährliche Regionen und Prozeduren: wo sich besondere Vorsicht empfiehlt.
06.06.18 Grundvoraussetzung der Idee für die Legitimation der Anwendung des Tertium non datur ergänzt. * Linkfehler korrigiert.
12.09.15 Beweisfehler Poincaré 1889 * Beweismethode vollständige Induktion *
21.03.15 Linkfehler geprüft und korrigiert.
12.03.15 Linkfehler geprüft und korrigiert.
21.12.11 Beweisfehler bei John von Neumann u.a.
20.08.09 Beweisfehler Fundamentalsatz der Algebra > Gauß.
16.08.09 Falsche Beweise von Hensel.
20.09.08 Frege Kritik an Hilbert.
31.01.08 Ruffinis Lücke nach Pesic (2005) Abels Beweis.
20.11.07 Link zu ONE HUNDRED AND TWO PROBLEMS IN MATHEMATICAL LOGIC.
18.07.07 Antinomisch- paradoxe Problematik des Reflexivitätsbegriffs (unter). * Alle und jeder Fallstrick.
15.07.07 Nachträge Beweisfehler.
12.07.07 Liouville entdeckt Fehler im 'Beweis' des großen Fermatschen Satzes von Lamé (1847).
06.07.07 Exkurs V: Mehr oder minder gut beweisen?
01.07.07 Tschebyschow Beweislücken.
21.06.07 Hilbert über den Steinerschen Fehlschluss und eine Fehlertheorie.
13..06.07 Russell über seine Erfahrung mit der Güte mathematischer Beweise.
08.06.07 Ergänzungen IV., Hinweis Geschichte Grundlagenstreit.
25.05.07 Ergänzung: Kritik Poincarés an Hilberts Beweisführung.
17.05.07 Exkurs IV: Ist die Mathematik so sicher, wie sie sich präsentiert?
23.01.06 Du Bois-Reymond Zitat nach Cranz zu den Grundlagen der Mathematik um 1895.
14.12.05 Querverweis: Rabulistik und Sophistik in der altehrwürdigen Mathematik.
19.08.05 Literaturaufnahmen Friedman und Link: One Hundred And Two Problems In Mathematical Logic
08.11.04 Links: Materialien zur Kontroverse um das Unendliche * Unendlich Begriffe * Cantor-Probleme *
25.08.04 Fußnote zum Homonym Logistik.
10.01.04 Link mit direktem Beweisbeispiel zur Summe 1+2+3+...+n : http://de.wikipedia.org/wiki/Beweis_(Mathematik)