Internet Publikation für Allgemeine und Integrative Psychotherapie
(ISSN 1430-6972)
IP-GIPT DAS=04.05.2006 Internet-Erstausgabe, letzte Änderung: 18.01.20
Impressum: Diplom-PsychologInnen Irmgard Rathsmann-Sponsel und Dr. phil. Rudolf Sponsel
Stubenlohstr. 20     D-91052 Erlangen * Mail: sekretariat@sgipt.org_Zitierung & Copyright_
Anfang_CST-Faktorenanalyse _Überblick  _Relativ Aktuelles  _ Rel. Beständiges  _Titelblatt  _Konzept  _Archiv  _Region _ Service iec-verlag __Wichtige Hinweise zu Links und Empfehlungen
Willkommen in der Abteilung Wissenschaftstheorie, Methodologie und Statistisch-Mathematische Methoden in der Allgemeinen und Integrativen Psychologie, Psychodiagnostik und Psychotherapie, hier:

CST - Charakter-Struktur-Test nach Riemann

Hauptkomponenten-Faktorenanalyse der Motivgruppen, Strukturen und der
Zusatzskalen Vitalität, Positiver Gefühlsanteil und Psychosomatische Belastung

[Zugleich: 3. Ergänzungslieferung zum CST-Testhandbuch 03-02-050.1 - Faktorenanalysen: Unauffällige N=214].

von Rudolf Sponsel, Erlangen



Zusammenfassung, Abstract, Summary.

In der folgenden Darstellung repräsentiert jede Spalte einen Faktor und in jeder Zeile stehen die Variablen. In jeder Zelle stehen die "Ladungen", d.h. die Korrelationen, also Zahlen zwischen -1 (maximal gegenläufiger Zusammenhang) und +1 (maximal gleichsinniger Zusammenhang), die den Zusammenhang zwischen Variable und Faktor anzeigen. Eine - mehr oder minder fette - Markierung bedeutet, dass ein entsprechend positiver Eintrag vorliegt. Negative Werte oder solche < 0.20 werden nicht markiert. Gibt es in einer Spalte keine Markierung, so spielt dieser Faktor keine Rolle, weil z.B. eine Fast-Kollinearität vorliegt, wie das z.B. unten bei den Gesamtwerten der Strukturen Z, H, S, D der Fall ist. Die folgende Darstellung und Terminologie orientiert sich an Überla (1971). Ein Hauptwert der Faktorenanalyse ist sicher, dass die Beziehungen der Variablen und Strukturen klarer und deutlicher hervortreten. Dies kann man unten sofort beim Vergleich der Korrelationsmatrizen und der Ladungsmatrizen sehen.

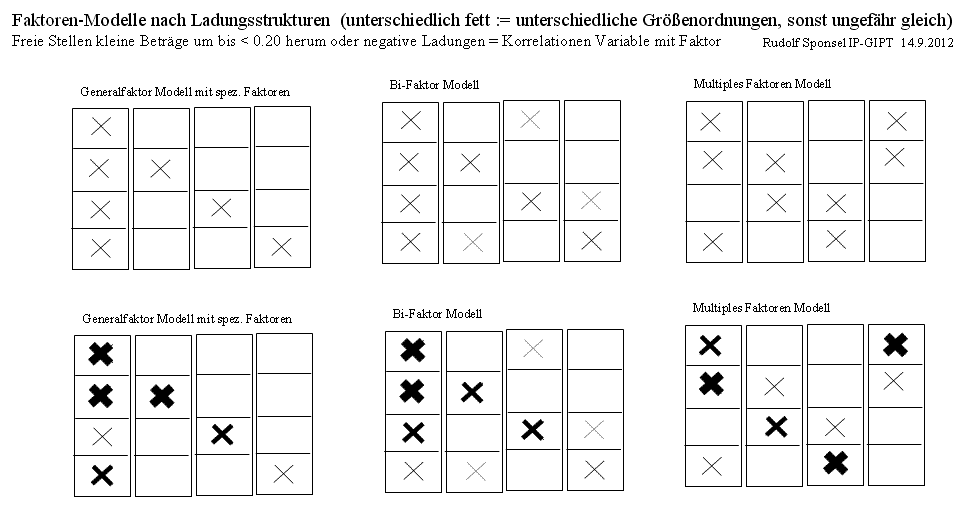
Der CST - Charakter-Struktur-Test nach Riemanns Grundformen der Angst wurde von Sponsel (1981) in einer Testversion operationalisiert. Hierbei wurden die 4 Grundstrukturen Z, H, S und D mit je 20 Items in 17 Motivgruppen aufgeteilt. Die faktorielle Gültigkeit sowohl der 4 Strukturen als auch der 17 Motivgruppen wird bei einer Stichprobe von N=214 Unauffälligen durch eine Hauptkomponenten-Faktorenanalyse der Korrelationsmatrix belegt. Und zwar ohne Rotation, weil diese einen unzulässigen Eingriff in die Bedeutungsstruktur (Vorzeichen und Betrag) der Korrelationen der Variablen mit den Faktoren bewirkt (> Relationentreue). Nachdem die vier Strukturen Z, H, S, D mit den durch sie konstituierenden Motivgruppen (artefiziell) linear abhängig sind, sind vier Eigenwerte (praktisch "nahe") 0 zu erwarten. Drei der Eigenwerte sind ab der 4. Nachkommastelle oder "später" negativ, so dass bei multivariater Weiterverarbeitung imaginär-komplexe Werte und mögliche Entgleisungen z.B. bei den multiplen Korrelationskoeffizienten resultieren, wenn man sie nicht 0 setzt (hier aus Demonstrationsgründen nicht gemacht).

Wie man sieht, ist die Grundforderung eines Generalfaktors für alle vier Strukturen erfüllt. Und in jeder Spalte wirkt wenigstens ein spezifischer Faktor. Das ist insofern erstaunlich als der CST rein inhaltlich-theoretisch konstruiert wurde - allerdings mit großem Aufwand (siehe CST-System Handbuch 03-02-050-01 bis 26). Man kann dieser Studie sehr schön entnehmen, dass Mathematik, Statistik und Faktorenanalyse "mitspielen" und verständlich interpretierbar angewendet werden können, wenn die Inhalte entsprechend sorgfältig fundiert und entwickelt werden und man auf dubiose Kommunalitäts- und Rotationsmethoden verzichtet. Alle vier Strukturen bestehen aus einem jeweiligen Struktur-Generalfaktor und spezifischen Motivgruppenfaktoren, wenn auch nicht alle Operationalisierungen zu einer vollständig ideal gewünschten Faktorladungsverteilung führen. Aus formalen Gründen ist ein spezifischer Faktor im Generalfaktor enthalten, denn jede n*n-Matrix hat nur n Faktoren und wenn eine Spalte vom Generalfaktor belegt ist, sind nur noch n-1, hier also 3 übrig.

Zur Bedeutung und Interpretation der Faktorenladungen
Zum Problem der Dimensionsanalyse

Die Hauptkomponenten-Faktorenladungen geben die Korrelation zwischen Faktoren und Variablen an. Daher sind alle Manipulationen, die das Vorzeichen oder die Beträge deutlich verändern unzulässige Eingriffe, die die Relationentreue massiv verletzen. Die Beliebigkeit mit der durch beliebige orthogonale Rotationen unendlich viele "richtige" mathematische Lösungen erzeugt werden können -  d.h. solche, die die Korrelationsmatrix richtig reproduzieren können -  hat mit Wissenschaft nichts, mit Numerologie und esoterisch-szientistischer Zahlenmystik sehr viel zu tun. Eine angemessene Reproduktion der Korrelationsmatrix ist grundsätzlich nicht möglich, wenn die 1en der Hauptdiagonale verstümmelt aus den faktorenanalytischen Schlachthäusern und Folterkammern zurückkehren. Jede Korrelationsmatrix ist I. phänotypisch gesehen symmetrisch, hat in der Hauptdiagonale 1en und den Zellen -1 <= Werte <= +1 stehen; II. gehört genotypisch notwendig dazu, dass die Korrelationsmatrix  semipositiv definit ist, d.h. für alle Eigenwerte muss idealiter gelten, dass sie >= 0 sind und die Summe der Eigenwerte muss gleich der Ordnung der Matrix oder der Summe der Diagonalelemente sein. Das gilt für keine Kommunalitätsmatrix (Rh). Daher kann eine Kommunalitätsmatrix auch niemals eine Korrelationsmatrix repräsentieren. Der Datenreduktionsfuror ist nunmehr ein über 100jähriger Irrläufer und genau betrachtet ein wissenschaftliches Wahnsystem auf dem Niveau der Astrologie, allerdings gut mathematisch-szientistisch verkleidet.

Interpretationsvorbehalt (Begründung: Simulationsversuch)
Die folgenden Interpretationsregeln gelten vorbehaltlich, da erste Simulationsversuche ergeben haben, dass Fälle auftreten, die auch mit der Hauptkomponentenmethode ohne die üblichen faktorenanalytischen Malträturen der Hauptdiagonalelemente oder des Eigenwertwegwerfens nicht vernünftig interpretierbar sind

  1. In der Faktorenladungsmatrix sind gewöhnlich die Faktoren in den Spalten und die Variablen in den Zeilen angeordnet.
  2. Grundlegender erster Schritt: Man betrachtet die Spalte eines Faktors und sieht nach, bei welchen Variablen er merkliche, deutliche oder gar hohe positive Ladungen aufweist. Solche um 0 (Faustregel < 0.20) oder negative beachte man für die Erstinterpretation nicht.
  3. "Lädt" ein Faktor auf allen Variablen positiv, spricht man von einem Generalfaktor.
  4. Spielen weitere Ladungen (>= 0.20)  neben einem Generalfaktor eine Rolle, spricht man von einem Bifaktor-Modell, ansonsten von multiplen Faktoren-Modellen (siehe bitte oben Modell-Graphiken).
  5. Zeigt ein Faktor nur bei einer Variablen eine hohe Ladung, so kann dieser Faktor mit der Bedeutung der Variablen, auf der er hoch lädt, identifiziert werden.
  6. Zeigt er auf mehreren Variablen höhere Ladungen, so handelt es sich um einen sog. "gemeinsamen Faktor" und dieser bedeutet dann das den Variablen Gemeinsame, auf denen er merklich lädt.
    Am 13.9.12 wurde die Faktorenanalyse des CST nach vorangehenden und grundsätzlichen Überlegungen zur Bedeutung der Vorzeichen bei den Faktorenladungen in der Hauptkomponentenanalyse (PCA) teilweise neu interpretiert.


Interkorrelationsmatrix (Gesamtmatrix) CST mit Zusatzskalen Unauffällige N=214



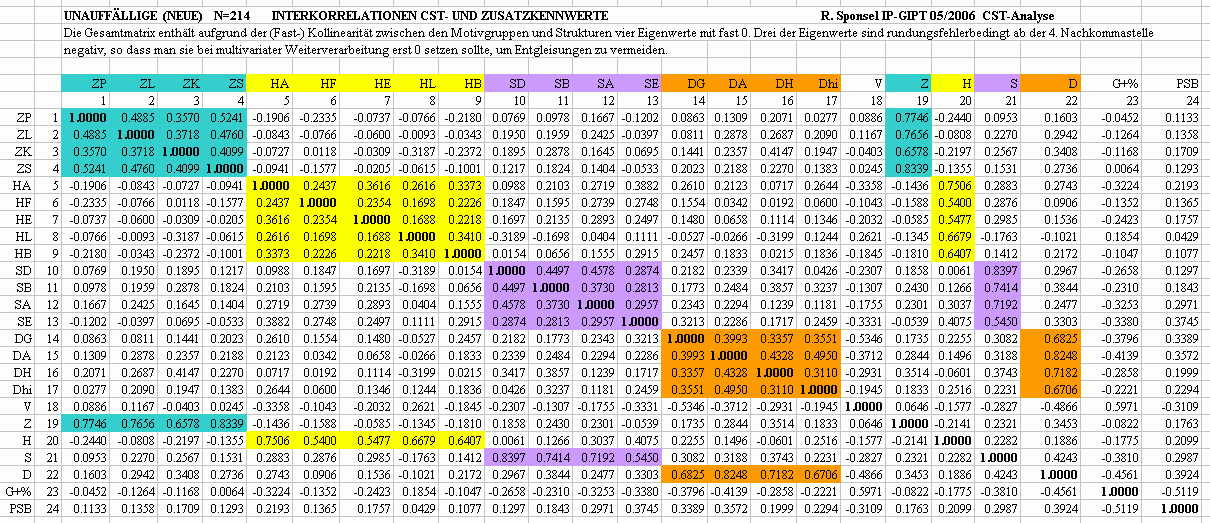
Faktorenladungen der Gesamtmatrix mit vier artefiziellen Fast-Kollinearitäten

In der 24*24 Gesamtmatrix sind die 17 Motivgruppen, die Zusatzskala Vitalität (V) oder Ich-Stärke, die 4 Strukturen Z, H. D und D und die zusätzlichen "Gesundheitsskalen" Positives Gefühlsverhältnis (G+) und Psychosomatische Belastung (PSB) enthalten. Die Gesamtmatrix enthält aufgrund der linearen Abhängigkeit der 4 Strukturen von den sie konstituierenden 17 Motivgruppen vier lineare Abhängigkeiten (Kollinearitäten), was sich in vier Eigenwerten nahe 0 ausdrückt. Rundungsfehlerbedingt sind drei der vier Eigenwerte ab der 4. Nachkommastelle oder weiter negativ, wodurch es bei der Berechnung der Faktorenladungen zu geringfügig imaginären Werten ("fast" 0) kommt, die aus demonstrativ-didaktischen Gründen hier so, wie sie sich ergaben, mitgeteilt werden. Bei Entgleisungsgefahr muss man sie 0 setzen (Sponsel, 1994:, Kap. 5: "Therapiemethoden indefiniter Korrelationsmatritzen"). Man mache sich auch klar, dass Eigenwerte nahe 0 gerade kein "Rauschen", gerade keine "Fehler" bedeuten, oder einfach zum "Wegwerfen" sind, sondern dass Eigenwerte nahe 0 eine gesetzesartige Regelhaftigkeit vom Typ (fast-) linearer Abhängigkeit (Kollinearität) bedeuten: man hat quasi ein "Gesetz" gefunden, wofür die FaktorenanalytikerInnen in der Psychologie aber gewöhnlich blind sind. In unserem Falle ist die Kollinearität der Motivgruppen mit dem Gesamtwert der Gruppe allerdings artefiziell und sozusagen qua Konstruktion hergestellt. Das ist zwar theoretisch lehrreich, aber natürlich keine empirische Entdeckung. Inhaltlich heißt das nichts anderes, als dass die gesamte Information bereits in den jeweiligen Motivgruppen enthalten ist und der Gesamtwert keine weitere Information mehr liefert. Wenn man vier Körbchen hat, in denen sich 1, 2, 3, und 4 Brötchen befinden, und man stellt diese vier Körbchen in eine Schachtel, so enthält diese Schachtel 10 Brötchen. Das weiß man aber schon, wenn man die Brötchen in den vier Körbchen zählt. Genau dieser Fall liegt bei den Motivgruppen und dem jeweiligen Strukturgesamtwert vor und deshalb ist ein Eigenwert - bis auf Rundungsfehler - Null..

Der CST umfaßt 100 Items, je 20 sind den Strukturen Z, H, S, D und V (Vitalität = Ichstärke) zugeordnet. Der CST besteht also aus vier Strukturen mit jeweils 4-5  Motivgruppen, die durch inhaltliche Überlegung (> CST-System Handbuch) aus 3 bis 7 Items gebildet wurden. Durch Einbeziehung des jeweiligen Gesamtwertes einer Struktur kommt eine artefizielle Kollinearität in die Korrelationsmatrix, was sich durch einen Eigenwert von 0 zeigt. Durch Rundungsfehler der hochgradig instabilen oder positv-semidefiniten Korrelationsmatrix sind einige Ladungen imaginär, was sich aber hier nicht weiter störend auswirkt und hier aus Demonstrationsgründen bewusst so belassen und dargestellt wurde.
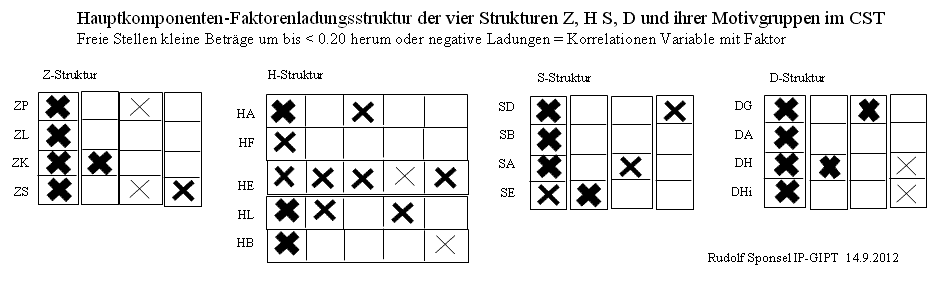
    Die Motivgruppen-Faktorladungsmatrix sollte jeweils einen Generalfaktor aufweisen, der sozusagen in allen Motivgruppen wirksam ist. Ein solcher zeigt sich in durchgängig deutlich positiven Faktorladungskorrelationen. Daneben sollte es idealiter jeweils eine hervorstechende positive und spezifische Motivgruppenfaktorladung geben, während die anderen idealerweise bei 0 liegen. Negative Vorzeichen zeigen eine negative Korrelation des Faktors mit der Variablen an.
    Rotationen können sowohl die Vorzeichen als auch die Beträge der Korrelationen des Faktors mit der Variablen drastisch verändern und sind daher als unzulässige Verletzung der Relationentreue abzulehnen.


Die Hauptkomponenten-Faktorenladungen  der Z-Struktur
Z-Struktur ("zwanghaft"): ZP=Z-Perfektionsstreben, ZL=Z-Leistungsbereitschaft, ZK=Z-Kontrolle, ZS=Z-Sicherheitsstreben.

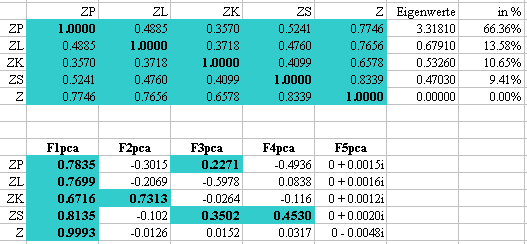
Die Faktorenladungs-Matrix der vier Motivgruppen ZP, ZL, ZK, ZS zeigt mit dem ersten Faktor einen sehr deutlichen Generalfaktor, der schon durch die Eigenwertstruktur nahegelegt wird, der größte Eigenwert schöpft  66.36% der Varianz aus und alle anderen vier liegen in einer ähnlich kleinen Größenordnung. Die Korrelationsmatrix mit dem Gesamtwert Z enthält eine artefizielle Kollinearität, was sich durch einen Eigenwert 0 ausdrückt. Kleine Eigenwerte sind also nicht einfach zu vernachlässigen, sondern sie drücken eine gesetzesartige Regelhaftigkeit vom Typ lineare (Fast-) Abhängigkeit (Kollinearität) aus, wie man hier unmittelbar sehen und nachvollziehen kann.
    Der zweite Faktor kann direkt als Z-Kontrolle identifiziert werden, weil er mit der Variablen Z-Kontrolle mit 0.7313 positiv korreliert. Die 3. Faktor korreliert eben merklich mit Z-Perfektion, schwach positiv mit Z-Sicherheit. Der 4. Faktor zeigt eine mäßig positive Korrelation mit Z-Sicherheit bei deutlich negativer Korrelation mit Z-Perfektion. Dadurch kann man zwei Varianten der Z-Sicherheit vermuten: eine die über die Perfektion geht und eine allgemeine (die gerade mit Perfektion negativ korreliert).


Die Hauptkomponenten-Faktorenladungen der H-Struktur
H-Struktur ("hysteroid"): HA=Anspruchshaltung, HF=H-Freiheitsstreben (äußeres), HE=H-Erlebnishunger, HL=H-Lebendigkeit, HB=H-Beeindruckung.

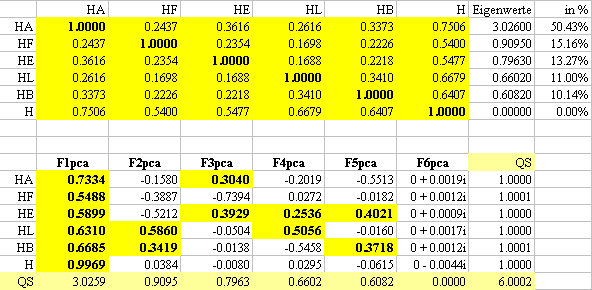
Die fünf Motivgruppen HA=Anspruchshaltung, HF=H-Freiheitsstreben (äußeres), HE=H-Erlebnishunger, HL=H-Lebendigkeit, HB=H-Beeindruckung der H-Struktur zeigen mit dem ersten Faktor einen klaren und ausgeprägten Generalfaktor H an, was sich schon an der Eigenwertstruktur zeigt, der größte Eigenwert  schöpft 50.43% der Varianz aus und alle anderen vier liegen in einer ähnlich kleinen Größenordnung. Der Ladungen beim Gesamtwert sind praktisch 0. Im Faktor 6 werden aufgrund der artefiziellen Kollinearität im Zusammenspiel mit Rundungsfehlern imaginäre Werte um 0 angezeigt.
    Der 2. Faktor lädt deutlich bei H-Lebendigkeit und mäßig bei H-Beeindruckung, die man beide auch als Extraversionsfaktoren bezeichnen könnte. Der dritte Faktor lädt mäßig bei H-Anspruchshaltung und bei H-Erlebnishunger. Der 4. Faktor lädt deutlich bei H-Lebendigkeit und eben merklich bei H-Erlebnishunger. Der 5. Faktor lädt mäßig bei H-Erlebnishunger und bei H-Beeindruckung.


Die Hauptkomponenten-Faktorenladungen der S-Struktur
S-Struktur ("schizoid"): SD=S-Distanz (Autonomie), SB=S-Beherrschung, SA=S-Aggression, SE=S-Entfremdung (Identitätsstreben).

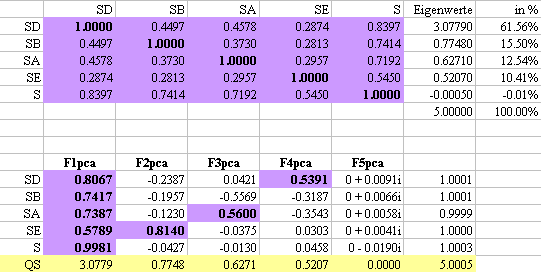
Die vier Motivgruppen SD=S-Distanz (Autonomie), SB=S-Beherrschung, SA=S-Aggression, SE=S-Entfremdung (Identitätsstreben) zeigen mit dem ersten Faktor einen klaren und ausgeprägten Generalfaktor S an, was sich schon an der Eigenwertstruktur zeigt, der größte Eigenwert schöpft 61.56% der Varianz aus und alle anderen vier liegen in einer ähnlich kleinen Größenordnung. Formal liegt hier eine Idealverteilung vor: in jeder Spalte gibt es nur einen spezifischen Faktor.
    Faktor 2 lädt hoch auf S-Entfremdung, Faktor 3 lädt deutlich auf S-Aggression und Faktor 4 lädt deutlich auf S-Distanz. Faktor 5 hat imaginäre Einträge, die sich durch die artfizielle Kollinearität des Gesamtstrukturwertes S im Zusammenhang mit Rundungsfehlern erklären. S-Beherrschung denke ich mir im Generalfaktor enthalten.


Die Hauptkomponenten-Faktorenladungen der D-Struktur
D-Struktur ("depressiv"): DG=D-Geborgenheit, DA=D-Anpassung, DH=D-Harmonie, DHi=D-Hingabe.

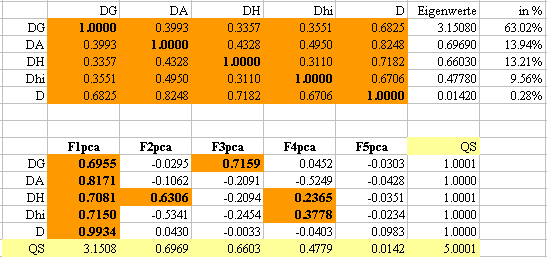
Die vier Motivgruppen DG=D-Geborgenheit, DA=D-Anpassung, DH=D-Harmonie, DHi=D-Hingabe zeigen mit dem ersten Faktor einen klaren und ausgeprägten Generalfaktor D an, was sich schon an der Eigenwertstruktur zeigt, der größte Eigenwert schöpft 63.02% der Varianz aus und alle anderen vier liegen in einer ähnlich kleinen Größenordnung.
    Die Korrelationsmatrix mit dem Gesamtwert D enthält eine artefizielle Kollinearität, was sich durch einen Eigenwert 0 ausdrückt. Kleine Eigenwerte sind also nicht einfach zu vernachlässigen, sondern sie drücken eine gesetzesartige Regelhaftigkeit vom Typ lineare (Fast-) Abhängigkeit (Kollinearität) aus, wie man hier unmittelbar sehen und nachvollziehen kann.
    Faktor 2 lädt sehr deutlich bei D-Harmonie, Faktor 3 lädt noch ausgeprägter bei D-Geborgenheit und Faktor 4 lädt schwach merklich bei D-Harmonie und mäßig bei D-Hingabe.
 


Hauptkomponenten-Faktorenanalyse der vier Strukturen Z, H, S und D
Zum Problem der Dimensionsanalyse

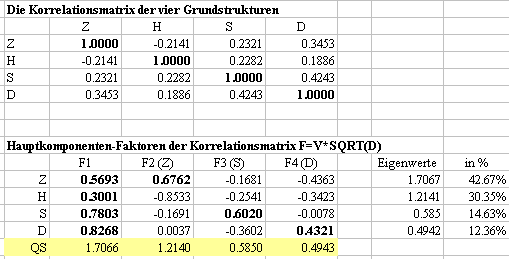
Nach den oben aufgestellten Regeln liegt ein Generalfaktormodell mit spezifischen Faktoren vor. Faktor 2 lädt auf Z, Faktor 3 auf S und Faktor 4 auf D mit jeweils einzig positiv deutlicher Ladung. H kann oder muss also im Generalfaktor enthalten gedacht werden.
Während in der Korrelationsmatrix die Strukturen D und Z positiv korrelieren (0.3453), ist das bei den Faktoren umgekehrt (-.4363).
Z lädt auf mit 0.0037, also ein unkorrelierter Zusammenhang.
D und S sind in der Korrelationsmatrix positiv korreliert(.4243), in der Faktorenladungsmatrix unkorreliert (-.0078).
Die Ladungen im Generalfaktor sind unerwartet hoch und so gesehen in ihrer Ausprägung nicht einfach zu verstehen.

Simulationsversuch einer idealtypischen Eigenwertstruktur, der zu denken gibt
Intuitiv ideal erscheint für vier voneinander unabhängige und gleichgewichtige Strukturen A, B, C, D eine annähernd gleiche Eigenwertverteilung. Idealtypisch wäre eine Faktorenstruktur vom Typ Einheitsmatrix. Die Interpretation wäre klar: Jeder Faktor lädt in jeder Variable maximal, also mit 1. Das führt zu einer Korrelationsmatrix, die wie eine Einheitsmatrix aussieht. Alle Eigenwerte sind exakt 1. Die Eigen-Vektoren haben 1en in der Nebendiagonale wie auch die Faktorenladungsmatrix. Ändert man die Eigenwerte dem Anschein nach nur gering ab, statt vier 1en 1.05, 1.02, 0.98 und 0.95, so möchte man intuitiv eine relativ ähnliche Faktorenladungsmatrix erwarten. Wie man indessen sehen kann, unterscheiden sich beide Faktorenladungsmatrizen sehr erheblich:

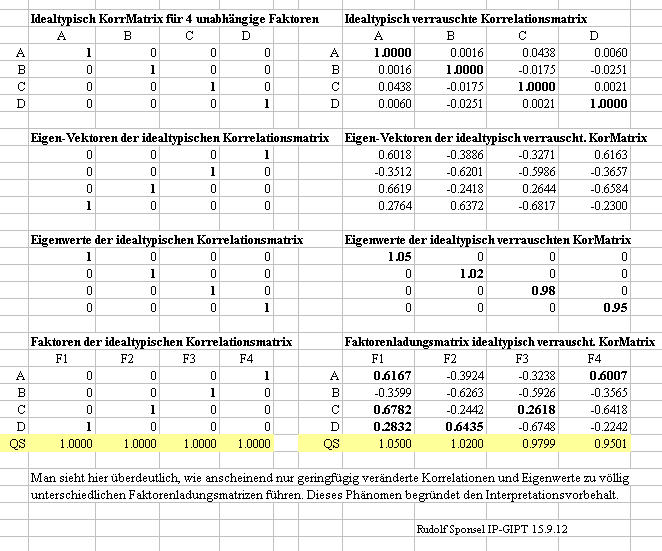
Man sieht der aus den Eigenwerten 1.05, 1.02, 0.98 und 0.95 konstruierten Korrelationsmatrix sofort an, dass die vier Variablen A, B, C, D  - analog den vier Strukturen  Z, H, S, D im CST - praktisch unkorreliert sind, weil alle Belegungen außerhalb der Hauptdiagonalen um 0 herum schwanken (die  höchste Korrelation ist gerade mal 0.0438. Man sollte also ein Faktorenladungsmuster ähnlich der idealtypischen Nebendiagonalmatrix erhalten, zumindest habe ich das erwartet. Obwohl die Abweichungen der Eigenwerte und der Korrelationsmatrizen gering erscheinen, wird hier doch eine völlig unerwartete Hauptkomponenten-Faktorenladungsmatrix erzeugt: mit 6 statt 4 deutlich positiven Ladungen und einem Durcheinander der Belegungen: Für B scheint es keinen Faktor zu geben, aber der Faktor 1 lädt gleich drei mal in A, C und D. Und auf  D laden sowohl F1 als auch F2, ebenso bei A, wo F1 und F4 laden. Und genau dieses Phänomen begründet den Interpretationsvorbehalt.

Fazit Simulationsversuch: Wieder einmal zeigt sich, dass scheinbar geringe Abweichungen, enorme Auswirkungen haben. Das genau ist das Wesen der - hier numerischen - Instabilität. Kleine Auswirkungen beim Input, hier bei den Eigenwerten im Vergleich zur Einheitsmatrix, haben auf die Faktorenladungen extremen Einfluss. Das erscheint als ein großes Problem, das an die Verwendung der Hauptkomponentenmethode neue Herausforderungen stellt. Mathematik, die in der Anwendung nicht vernünftig interpretiert werden kann, ist letztlich kaum zu gebrauchen.
    Dieses Ergebnis steht in einem gewissen Widerspruch zum Fehlerversuch (Überblick, Basisdaten und Versuchsplan, Beispiel 50% Fehlerspannweite). Dort wurden auf einen als wahr definierten Datensatz systematisch normalverteilte Fehler hinzugegeben (bis zu 1.000.000 %), wobei sich die Eigenwerte und ihr Verlauf weitgehend robust und wenig verändert zeigten.


Literatur (Auswahl): siehe bitte.
  • Sponsel, Rudolf & Hain, Bernhard (1994). Numerisch instabile Matrizen und Kollinearität in der Psychologie. Diagnose, Relevanz & Utilität, Frequenz, Ätiologie, Therapie.  Ill-Conditioned Matrices and Collinearity in Psychology. Deutsch-Englisch. Ins Englische übersetzt von Agnes Mehl. Kapitel 6 von Dr. Bernhard Hain: Bemerkungen über Korrelationsmatrizen. Erlangen: IEC-Verlag [ISSN-0944-5072  ISBN 3-923389-03-5]. Aktueller Preis: www.iec-verlag.de.
  • Sponsel, R. (2005). Fast- Kollinearität in Korrelationsmatrizen mit Eigenwert-Analysen erkennen. Ergänzungsband - Band II zu Numerisch instabile Matrizen und Kollinearität in der Psychologie. Erlangen: IEC-Verlag.

    • Links (Auswahl: beachte)

    Glossar, Anmerkungen und Endnoten:
    1) GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
    ___
    Drei der Eigenwerte:

    Querverweise
    Standort: Hauptkomponenten-Faktorenanalyse CST - Charakter-Struktur-Test.
    *
    Kommunalität * Zum Problem der Dimensionsanalyse
    Überblick der Dokumentationen zur Handhabung der Faktorenanalyse
    Kritik der Handhabung der Faktorenanalyse
    Was für ein Typ Matrix entsteht durch Faktorenanalysen?
    Überblick Numerisch Instabile Matrizen und Kollinearität in der Psychologie
    Zahlenmystik und numerologische Esoterik in Statistik und Testtheorie
    Überblick Arbeiten zur Definitionslehre, Methodologie, Meßproblematik, Statistik und Wissenschaftstheorie
    *
    *
    Dienstleistungs-Info.
    *

    Zitierung
    Sponsel, Rudolf  (DAS). CST - Charakter-Struktur-Test nach Riemann. Hauptkomponenten-Faktorenanalyse der Motivgruppen, Strukturen und der Zusatzskalen Vitalität, Positiver Gefühlsanteil und Psychosomatische Belastung. IP-GIPT. Erlangen: https://www.sgipt.org/wisms/fa/cst/cst214U.htm
    Copyright & Nutzungsrechte
    Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht  inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das Einbinden in fremde Seiten oder Rahmen ist nicht gestattet - Links sind natürlich willkommen. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus  ...  geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.


      Ende_CST-Faktorenanalyse_ Überblick  _ Relativ Aktuelles  _ Rel. Beständiges  _ Titelblatt  _ Konzept  _  Archiv  _ Region _ Service iec-verlag _ Mail:sekretariat@sgipt.org  ___Wichtige Hinweise zu Links und Empfehlungen
    kontrolliert am: irs 14.09.2012

    Änderungen wird gelegentlich überarbeitet, ergänzt und vertieft * Anregungen und Kritik willkommen
    16.04.13   Linkfehler Relationentreue korrigiert.
    15.09.12    Vollständige Überarbeitung und Neuinterpretation, insbesondere im Hinblick auf die Bedeutung der Vorzeichen bei den Ladungen, Simulationsversuch und Interpretationsvorbehalt.
    05.06.06    Zum Problem der Dimensionsanalyse
    11.05.06    Faktorenanalyse der vier Strukturen.