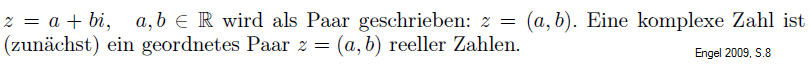(ISSN 1430-6972)
IP-GIPTDAS=12.08.2016 Internet Erstausgabe, letzte Änderung: 29.09.16
Impressum: Diplom-Psychologe Dr. phil. Rudolf Sponsel Stubenlohstr. 20 D-91052 Erlangen
Mail:_sekretariat@sgipt.org_ Zitierung & Copyright
Anfang_ Komplexe & Imaginäre Zahlen_ Rel. Aktuelles _Überblick_Überblick Wissenschaft _Rel. Beständiges_ Titelblatt_Konzept_Archiv_Region_Service iec-verlag___ _Wichtige Hinweise zu Links und Empfehlungen
Willkommen in unserer Internet-Publikation für Allgemeine und Integrative Psychotherapie, Abteilung Wissenschaft, Bereich Mathematik und hier speziell zum Thema:
Die Sprache der Mathematik am
Beispiel
komplexe & imaginäre
Zahlen
aus der Sicht eines mathematisch interessierten Laien
Hilfsbegriffe Metamathematik - Die Sprache der Mathematik.
von Rudolf
Sponsel, Erlangen
__
Das mag sein, aber haben Mathematik und die Mathematik-Didaktik nicht einen sehr großen Anteil daran? Siehe Zusammenfassung-2.
Zusammenfassung-1
Irritationen beim Lernen der
komplexen & imaginären Zahlen
Hintergrund der Arbeit ist, dass mir vor ein paar Jahrzehnten mal ein
Mathematiker (Volkhard Rührig)
sein Bedauern ausgedrückt hat, dass ich den Hauptsatz der Algebra
ohne die komplexen Zahlen nicht verstehen könne. Diesen Mangel wollte
ich nun beheben, daher begann ich, mich mit den komplexen Zahlen zu beschäftigen.
Das Gebiet erscheint mir mehr als komplex ;-), was perfekt zur Namensgebung
passt. So ist wohl auch nicht verwunderlich, dass ich dabei auf einige
Verständnisschwierigkeiten gestoßen bin, die mich nun veranlassten,
meine Probleme hier aufzuschreiben und darzustellen. Zur leichteren Bezugnahme
habe ich meine "Irritationen" einfach durchnumeriert.
Eine Hintergrundirritation - lange vor der nun ausgiebigeren
Beschäftigung - ergab sich, dass eine Zahl nicht mehr "eine"
Zahl,
sondern zusammengesetzt, die Summe aus "zwei" Zahlen war. In meinen Gedanken
gab es einen Widerstand, ein Sträuben, zwei Zahlen (eigentlich sind
es ja drei: a, b, i) als "eine" Zahl anzusehen.
1. Irritation In nahezu allen
Mathematikbüchern und Lexika steht: Eine komplexe Zahl ist als Paar
reeller Zahlen der Form
z = a + bi definiert, wobei a
und b reelle Zahlen sind, a der Realteil und
b
der Imaginärteil heißt. Was in diesem Ausdruck a + bi oder a
+ ib nun genau was ist, wird unterschiedlich dargestellt. Irritiert hat
mich, dass so, wie es doch dort steht, bi und nicht nur
b
der Imaginärteil ist. Genau genommen besteht die formale Definition
aus drei Teilen: a, b, i. Der Imaginärteil ist
das Produkt aus der reellen Zahl b und der sog. imaginären Einheit
i wodurch bi zu einer imaginären Zahl wird. Beides, also das Produkt
bi, heißt Imaginärteil.
2. Irritation Sie bestand
darin, dass als Lösung der Gleichung x^2 = -1 der Buchstabe
i angegeben wird. Aber i ist nach meinem Verständnis
keine Lösung, sondern ein bloßes Definiendum
oder Symbol, wenn auch offenbar sehr nützlich. Ich suchte nach einer
Ergebnislösung für WURZEL(-1), das so, wie es dem Definiendum
i zugeordnet wird, ja noch eine auszuführende Aufgabe und keine Lösung
ist. Die Abkürzung i erscheint lediglich als technisch-symbolisches
Rechen-Hilfsmittel. Das hat mich insofern besonders irritiert, weil ja
in nahezu jeder Abhandlung über die komplexen Zahlen zu lesen ist,
dass man eine Lösung für die Gleichung x^2+1 = 0 sucht,
die es im Reellen nicht gibt.
3. Irritation Im Zusammenhang
mit der 2. Irritation stellte sich für mich somit die Frage: Was bedeutet
die imaginäre Einheit nun genau? .
4. Irritation Was kommt denn
nun heraus, wenn man die Quadrat-Wurzel aus einer negativen reellen Zahl,
hier speziell WURZEL(-1) zieht? Merkwürdigerweise findet man diese
Frage in den meisten Abhandlungen zu den komplexen Zahlen nicht beantwortet.
Auf meine Frage in de.sci.mathematik erhielt ich die Antwort i
und -i, die für mich nicht nur unbefriedigend war, sondern die
ich auch für falsch halte, obwohl das offenbar in der Mathematik gängige
Lehre ist: Die Lösungen der Gleichung WURZEL(-1) seien i
und -i. Bei Matlab wird allerdings nur i nicht -i, dafür
mit reellem Faktor 1 ausgegeben.
5. Irritation Sie ergab
sich dadurch, dass ich meine "Lösung"
für i in den Mathematikbüchern, die ich befragt hatte,
nicht finden konnte. Gesucht ist "eine" Zahl, deren Produkt -1 ergibt.
Es liegt auf der Hand, dass dies nur die Zahlen +1 und -1 sein können,
also zwei Zahlen vom gleichen Betrag. Allgemein (+a) * (-a), a > 0. Als
erste Näherungs-Lösung für WURZEL(-a), a > 0 bietet sich
an (-1) * WURZEL(|-a|) und (+1) * WURZEL(|-a|). Nach diesen
Überlegungen bestünde die Quadratzahl aus zwei dem Betrag nach
gleichen Zahlen mit unterschiedlichen Vorzeichen, wobei die Multiplikation
aber dem Reellen entlehnt und daher nicht statthaft ist, weil wir uns außerhalb
des Reellen befinden. Berücksichtigt man die Multiplikationsregel
für die komplexen Zahlen (a,b)*(c,d) = ac - bd, ad + bc
so ergibt sich wie vorüberlegt:
(0 + 1) * (0 + 1) = 0 - 1, 0 + 0 = -1
(0 - 1) * (0 - 1) = 0 + 1, 0 + 0 = +1
6. Irritation Diese ist mehr
formal-technischer Natur. In meinem alten Bronstein (1981, 20. Auflage)
S. 558 wird Beta erst als Imaginärteil (0, Beta) deklariert, dann
aber in der Position des Realteils (Beta, 0) angewendet. Irritiert hat
mich: dass Beta anscheinend sowohl im Realteil als auch im Imaginärteil
verwendet wird.

Anmerkung Bronstein (1981) bezeichnet
ib (b für Beta) als rein imaginäre Zahl.
Mein Weg zum Hauptsatz der Algebra gestaltet sich
also etwas mühsam, wenngleich ich immer mehr staunte und bewunderte,
was z.B. Euler mit den imaginären Zahlen in seiner Zauberformel e^(i*pi)+1
= 0 schon 1748 geleistet hatte. Aufgrund der Irritationn habe ich ein Sichtung
aus der Literatur zu den imaginären und komplexen Zahlen vorgenommen.
Die Ergebnisse meiner Sichtung (Auswahl) finden Sie in Zusammenfassung-2.
Ich setze mit dieser kleinen Arbeit die Dokumentation meiner Irritationen und Schwierigkeiten mit der Sprache der Mathematik fort, quasi anknüpfend an meine vorangehenden Dokus (Kommutativität, Zählen).
Zusammenfassung-2 Ergebnisse der Sichtung mathematischer Texte zu den imaginären und komplexen Zahlen
Was heißt Imaginaerteil? Es herrscht grundlegende Unklarheit und Unsicherheit bis zur Widersprüchlichkeit, was in der algebraischen Normalform z = a + bi nun der Imaginärteil sein soll und was nicht. Im Einzelnen fand ich:
- Die Mehrheit (z.B. DIN 202, Engel, Kretzschmar, Wikipedia, Rottmann, ) sagt b sei reell und der Imaginärteil von z = a + bi. Das kann aber nicht richtig sein, weil, wenn b reell ist, eine reelle Zahl allein nicht der Imaginärteil sein kann, weil eine reelle Zahl nun einmal nicht imaginär ist..
- Einige sagen bi repräsentiere den Imaginärteil (Bronstein, Dittmann, dtv-Atlas Mathematik, Farkas, Kleiner Duden Mathe, Mückenheim, ).
- Manche widersprechen sich, weisen einmal b dann wieder bi als Imaginärteil aus (z.B. dtv-Atlas Mathematik b, bi).
- Manche lassen es offen und sagen b bzw. bi sei der Imaginärteil (so der Duden Rechnen und Mathematik 1994).
- Und schließlich kann man auch ausweichen und sich dazu nicht ausdrücklich äußern.
Was "ist" i und was ist WURZEL(-1)?
- i ist das Zeichen für WURZEL(-1). Nach den Regeln der Definitionslehre ist i das Definiendum und WURZEL(-1) das Definiens. In der Definitionslehre wird hierfür das Zeichen ":=" (so z.B. in Engesser, 1986, Imaginäre Zahlen, S. 207 ) "=def" oder auch "def" unter "=" verwendet. Der Ausdruck "i:=WURZEL(-1)" heißt, dass in allen Ausdrücken, in denen das Zeichen "i" verwendet wird, auch der Ausdruck "WURZEL(-1)" verwendet werden darf.
- Setzt man i=WURZEL(-1), dann bedeutet dies, dass WURZEL(-1) als Wertzuweisung zu interpretieren ist.
- Wurzelausdrücke sind mehrdeutig. Man kann z.B. mit WURZEL(2) erstens die unendliche Irrationalzahl meinen, die sich beim effektiven Wurzelziehen ergeben würde, wenn man nur fertig werden könnte, zweitens die Formulierung der Aufgabe, die Wurzel effektiv zu ziehen, drittens die Ausführung der Aufgabe, wobei man dann einen Näherungswert erhalten wird, z.B. 1,4142213562, so mein Taschenrechner, dessen Genauigkeit für die allermeisten Rechnungen genügen sollte. Und diese drei Bedeutungen gibt es auch bei WURZEL(-1). Erstens denkt man sich abstrakt-allgemein, dass es eine Lösung gibt. Zweitens formuliert man die Aufgabe durch hinschreiben, die WURZEL(-1) zu ziehen. Und drittens und letztens ist noch effektiv die WURZEL(-1) oder allgemein WURZEL(-a), a>0, reell zu ziehen.
Was heißt Loesung, insbesondere Loesung imaginaerer Quadratwurzeln WURZEL(-a), a>0, reell und speziell WURZEL(-1)
Schon Euler meinte (nach Dittmann 1981, S. 20), i sei die Lösung für WURZEL(-1). Und das wird von der großen Mehrheit der Mathematiker auch so gesehen. Aber, wenn i::=WURZEL(-1) oder per Wertzuweisung i=WURZEL(-1) gleichgesetzt wird, ist lediglich eine definitorische Abkürzung vorgenommen, aber keine Lösung der Aufgabe WURZEL(-1) erfolgt. Damit ist die Frage aufgeworfen: was ist eine Lösung, was soll eine Lösung heißen? Ich nehme noch einmal das Beispiel von oben: Was genau beschreibt der Ausdruck WURZEL(2)? Unkritische Platonisten meinen, da werde eine Zahl beschrieben, nämlich genau die Zahl, die mit sich selbst multipliziert 2 ergibt. Nun wissen wir aber, dass dies eine unendlich lange Zahl ist, und dass man unendlich lange Zahlen nicht aufschreiben und daher auch nicht mit sich selbst multiplizieren kann. Man muss sich mit Näherungswerten durch abschneiden begnügen, was ja auch praktisch kein Problem ist. Aber hier geht es nicht ums Praktische, sondern um die Frage: kann WURZEL(2) eine Lösung sein? Oder beschreibt nicht vielmehr WURZEL(2) eine Aufgabe? Analog stellt sich für WURZEL(-1) die Frage: kann das eine Lösung sein oder beschreibt das nicht die Aufgabe, die Zahlen zu suchen, die mit sich quadriert, -1 ergeben? Wie so oft zeigt sich auch hier wieder einmal, wie ungenau und schlampig der mathematische Sprachgebrauch ist, hier am Beispiel des Begriffes Lösung.
Obwohl fast jede Einführung in die komplexen Zahlen auf das eindrucksvoll einfache Beispiel x^2+1=0 verweist, oft mit der vollmundigen Erklärung diese Gleichung mit der Erweiterung der komplexen Zahlen zu lösen, sucht man sodann vergeblich nach einer tatsächlichen Lösung. Als Lösung wird nicht selten einfach i ausgegeben. Die "Lösung" besteht also darin, man ordnet dem Ausdruck WURZEL(-1) die Zahl i zu, also i := WURZEL(-1) und dazu sagt man dann "Lösung". Der zweite Teil der "Lösung" fällt auch oft unter den Tisch (-i) und um die Verwirrung komplett zu machen, lässt man auch noch den reellen Teil b, hier die 1, der Form bi weg.
21.08.2016 Die Mathematik lehrt: i = i und -i. In Worten: Die Lösungen aus WURZEL(-1) lauten +WURZEL(-1) und -WURZEL(-1). Es hat ca. vier Wochen - seit ich mich mit dem Lernen der komplexen Zahlen beschäftigte - gedauert, bevor ich diese Aussage nun so formulieren konnte. Inhaltlich akzeptieren kann ich diese "Lösungen" immer noch nicht, weil sich meine Vorstellung dagegen sperrt, dass das Ergebnis des Wurzel ziehens zur gleichen Zahl führen kann wie die Wurzel selbst. Auch als ich versuchte, mir mit der Analogie aus dem Reellen, die erste Ableitung aus e^x ist wiederum e^x zu helfen, wurde es nur etwas besser. Ich bin also noch nicht durch.
Zwischenstand-2 (04.09.2016)
(1) "i" wird einerseits als Symbolzeichen mit dem Namen "Imaginäre
Einheit", andererseits als Wert i=WURZEL(-1) gebraucht. Zugleich wird als
i und -i auch als Lösung für die Gleichung x^2+1=0
bezeichnet. i und -i
sind die Nullstellen dieser Gleichung. In der Tat: setzt man in x^2+1=0
ein WURZEL(-1) * WURZEL(-1) + 1 = 0 ergibt sich -1 + 1 = 0. Meine Irritationen
um die Bedeutung von "Lösung" sind damit beendet. Ich hatte
ständig nach einer Lösung gesucht, was denn herausraus kommt,
wenn man die Wurzel aus -1 tatsächlich zieht so wie die Wurzel(4)
eben 2 ergibt. Ich verstehe jetzt, was gemeint ist, enn man von i
und -i als Lösung spricht: es sind Nullstellen der Gleichung
x^2+1=0.
(2) Die Werte von i und -i lassen sich
herleiten aus (0,1)*(0,1) = 0 - 1, 0 + 0 = -1 bzw. (0,-1)*(0,-1) = 0 -
1, 0 + 0 = -1.
(3) Die Äquivalenz ib = (0, b) hat FF in dsm (July 12, 2016 at
5:00:17) noch einmal gezeigt: "Mit anderen Worten, es gilt also: ib = (0,
1)*(0, b). Nach den Rechenregeln für die komplexen Zahlen (siehe Bronstein-Zitat),
gilt dann also:
ib = (0, 1)*(0, b) = (0 * b - 1 * 0, 0 * 0 + 1 * b = (0, b)."
Neue Irritation:
(4) i^2=-1 lässt sich aus (0,1)*(0,1) = (-1,0) herleiten. Setzt
man i^2 in x^2 ein, ergibt sich i^2 + 1 = 0. Das Quadrat einer imaginären
Zahl ergibt eine reelle Zahl. Das kann man nach der Herleitung (0,1)*(0,1)
= (-1,0) nachvollziehen. Damit besteht der ganze Ausdruck i^2 + 1 = 0 aus
reellen Zahlen -1 + 1 = 0. Die komplexe Zahl x^2 + 1, wenn man i
in x einsetzt, besteht demnach aus lauter reellen Zahlen, obwohl sie im
Reellen keine "Lösung" hat und keine reelle Zahl ist.
Exkurs Kurzausflug in die Geschichte
der komplexen Zahlen
Beim Lösen von Gleichungen kam es vor, dass negative Werte in
Quadratwurzeln auftraten, die man mit den bekannten Mitteln nicht lösen
konnte, weil der Satz galt: eine Zahl mit sich selbst multipliziert ist
immer positiv, was im Widerspruch z.B. zu x=WURZEL(-4). Cardano (zit. nach
Pieper 1984, S. 193) formulierte 1545 die Aufgabe, die Zahl 10 so in zwei
Summanden zu zerlegen, dass das Produkt 40 ergibt (x1=5 + WURZEL(-15);
x2=5 - WURZEL(-15)). Als Paradebeispiel dient die Gleichung x^2+1=0 bzw.
x^2=-1 also x=WURZEL(-1). Lange Zeit wurden die imaginären Zahlen
als "unmögliche" Zahlen bezeichnet. In der Tat erscheint die Vorstellung,
dass eine Zahl, die mit sich selbst multipliziert, einen negativen Wert
ergibt, unmöglich. Und es gibt auch keine solche Zahl. Hingegen macht
die Vorstellung, dass eine Zahl +a mit -a multipliziert keine Probleme:
+1 * -1 = -1, +2 * -2 = -4, +4 * -4 = -16. Mit dieser Vorstellung
ist man bereits einer Lösung nahe, weil man ein Zahlenpaar betrachtet.
Indem man feststellte, dass sich die Ausdrücke manchmal weg kürzen
ließen und dann zu reellen Resultaten führten (Bombelli 1572
nach Pieper 1984, S. 195), waren die "unmöglichen" Zahlen letztlich
nicht störend. Aber das funktionierte nicht immer und die "unmöglichen"
Zahlen blieben lange Zeit unverstanden, obwohl man sie rechnerisch geschickt
anwendete - ein Beleg, wie nützlich Fiktionen in der Wissenschaft
und in der Mathematik sein können. Die Entwicklung der komplexen Zahlen
zog sich über 300 Jahre hin. Euler erfand die imaginäre Einheit
über i^2 = -1, woraus dann folgte: i = WURZEL(-1). Und er fand e^(i*phi)
= cos phi + i sin phi woraus sich die vielfach bewunderte Gleichung e^(i*pi)+1
= 0 ergab. Der Ausdruck imaginäre Zahl soll auf Descartes zurückgehen;
den Ausdruck komplexe Zahl hat Gauß 1831 eingeführt.
Er war bestrebt, den komplexen Zahlen aus ihrem nur geduldet sein
zum vollen Bürgerrecht zu verhelfen. Beispiel: Wurzel(-4) ist
im Reellen nicht lösbar, weil Quadrieren einer reellen Zahl immer
zu einer positiven - minus mal minus ist per definitionem
plus - reellen Zahl führen muss. Eine komplexe Zahl hat die (algebraische
Normal-) Form z = a - bi, wobei a als Realteil (reelle Zahl) bezeichnet
wird und bi als Imaginärteil mit b als reelle Zahl und i als imaginäre
Einheit.
Sprachregelung komplexe Zahlen nach DIN Taschenbuch 202 (1984), 1302, 4.-4.6
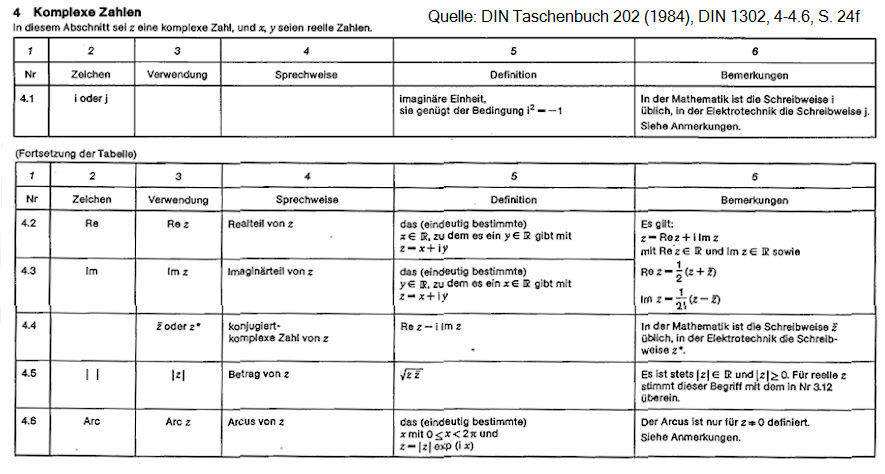
Kritik DIN 202 (1984)
Nach 4.3 ist nur y der Imaginärteil. Offensichtlich ist aber iy
der Imaginärteil (> Farkas,
dtv-Atlas,
Duden,
Mückenheim,
).
Neu scheint auch die Verknüpfung "mit z = x + iy" in
4.2 und 4.3, die hier nicht erklärt ist und dunkel bleibt. Wünschenswert
wäre zudem, dass der Körper der komplexen Zahlen an dieser Stelle
klar definiert wird.
Anmerkungen S. 37: "

Was heißt genau "imaginaere Einheit" und imaginäre Zahl?
Exkurs Vorueberlegung zum Begriff
der Einheit
In der Physik haben wir gelernt, dass eine physikalische Größe
aus einer Maßzahl und einer Einheit besteht.
Betrachtet man sich die Verwendung von i kann in der Tat der
Eindruck einer solchen Einheit nentstehen. Dazu habe ich aber in den von
mir eingesehenen Texten keine Ausführungen gefunden. Nachdem der Körper
der komplexen Zahlen lediglich durch i ergänzt wird, kann
man das so auffassen, dass jede komplexe Zahl mit Hilf eder reellen Zahlen
und der imagniären Einheit i dargestellt werden kann.
Man rechnet nicht mit der Lösung aus i=WURZEL(-1), sondern genau
mit dieser sog. imaginären Einheit. Irritierend ist, weshalb man dann
i als "Lösung" bezeichnet. WURZEL(-1) ist keine Lösung, sondern
die Aufgabe, genau der vorletzte Schritt, i ist ja bloß eine Abkürzung,
das Definiendum für das Definiens WURZEL(-1). Ich habe kein Problem
damit, dass es nützlich und sinnvoll ist, mit i zu rechnen.
Auch der Vergleich mit e hinkt, denn e ist ein
Zahlenwert, genauer ein Zahlenendwert, ein Ergebnis. So gesehen könnte
man i vergleichen mit der Aufgabe EXP(1). Klar ist weiter,
dass WURZEL(-1) keine reelle Zahl sein kann, weil es im Reellen keine Zahl
gibt, deren Quadrat negativ ist. Die mir in de.sci.mathematik mitgeteilten
"Lösungen" auf meine Frage nach dem Zahlenergebnis WURZEL(-1) mit
i und -i sind m.E. nicht nur unbefriedigend (im Grunde
zirkulär, analytisch wahr oder tautologisch), sondern auch falsch,
denn man sagt ja nur i = i.
- Verzicht auf die Nutzung des Begriffs "imaginaere
Einheit"
In Komplexe Zahlen für Dummies hat "imaginäre Einheit" keinen Sachregister-Eintrag und ich fand den Begriff auch sonst nicht im Text. Das ist insofern interessant, als es zur Einführung der komplexen und imaginären Zahlen nicht notwendig erscheint, den Begriff der "imaginären Einheit" einzuführen. S. 29 führt aus:

Imaginaere Zahlen
Kleiner Duden Mathe (1986)

Anmerkung: Hier wird das Definitionszeichen verwendet,
so dass also klar ist, i ist hier Definiendum, WURZEL(-1)
das Definiens. Außerdem wird die Form bi als imaginäre
Zahl bezeichnet, hier durch a * i.
- i als imaginaere Einheit
- Beispiele
Nach Lambacher Schweizer
(1967) Algebra 2 sind die Zahlenwerte, die i ^2 zugeschrieben werden,
das Ergebnis einer Definition:

Wieso eine "Definition" eine "Lösung" sein soll, bleibt unerklärt.
Mathematisches
Woerterbuch Naas & Schmid (1972, Hrsg.), Bd. 1, S. 946: i als imaginäre
Einheit.
Kein Eintrag unter I (1. Bd.). Unter dem Eintrag komplexe Zahl wird
zur imaginären Einheit ausgeführt:

Kritik Naas Die Zahl i ist keine
Lösung der Gleichung, sondern eine Bezeichnung oder ein Symbol für
WURZEL(-1), die für die Lösungen allerdings erst noch gezogen
werden müsste.
_
bi
als Imaginaerzahlen nach Dittmann (1981), S. 20

_
dtv-Atlas der Mathematik, 5. A. 1982, S.
65
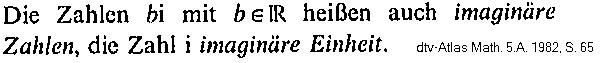
Anmerkung: Im Schaubild S. 64 zur Gaußschen
komplexen Zahlenebene wird nur b als imaginäre Zahl bezeichnet.
_
Farkas Herbstsemester 2014
(PDF
im Internet)

Imaginärteil
b bzw. bi im Duden Rechnen und Mathematik
a2 entspricht b bzw. a2i
entspricht bi.

Es ist also nicht klar und anscheinend beliebig, ob man nun b bzw.
bi
als Imaginärteil ansieht.
_
Rottmann (1991), S. 12

_
Walz (2003, PL)
Lexikon der Mathematik Spektrum, Bd. 2: i^2 als imaginäre Einheit.

_
Imaginaere Zahlen nach
Wikipedia

Kritik Wikipedia Der Imaginärteil sollte aus i * b bestehen, wobei b eine reelle Zahl ist.
- _
Definition bei Engel (2009)
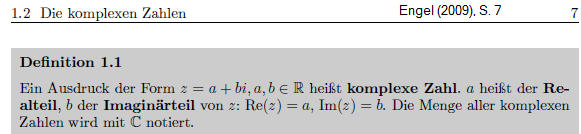
Kritik Def Engel Wieso verschwindet i aus dem Imaginärteil?
_
Definition bei Kretzschmar (2011)

_
Imaginaerteil bi nach Mueckenheim (2010) S. 37
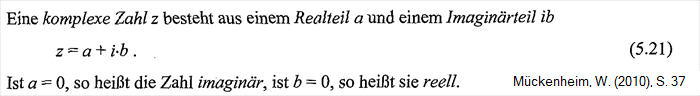
Die unterschiedlichen Darstellungsformen der komplexen Zahlen z
Die Bezeichnungen in der Literatur weichen teilweise voneinander ab. So spricht der dtv-Atlas von "Normaldarstellung", was hier Exponentialform heißt. Hier musste ich gelegentlich recht aufpassen, insbesondere wenn von der Darstellung geordnetes Paar zu anderen Darstellungen (algebraische Normalform, Polarform, Exponentialform) übergegangen wird (> Bronstein-Irritation).
- Geordnetes Paar reeller Zahlen z=(a,b).
- Algebraische Normalform z = a + bi = a + ib.
- Gaußsche komplexe Zahlenebene z = a + bi (geometrische Veranschaulichung).
- Polarform z = |z| (cos phi + i sin phi).
- Exponentialform z = |z| e^(i*ar(z)) mit arg(z) = 0, pi/2, pi, 3/2 pi.
- Moivre-Formel (cos phi + i sin phi)^n = cos n*phi + i sin n*phi.
- i als Drehoperator.
Komplexe Zahlen
als geordnetes Paar reeller Zahlen: z = (a, b)
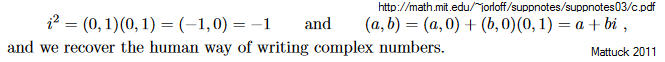
Gaußsche komplexe Zahlenebene z = a + bi
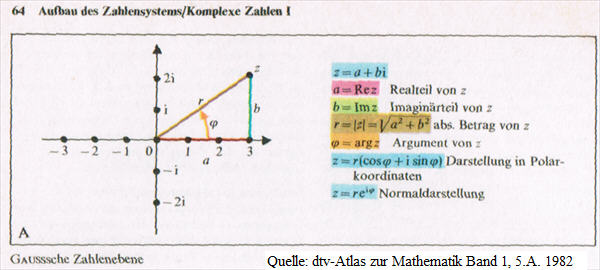
Kritik dtv-Atlas Hier wird nur b als Imiganärteil angegeben im Widerspruch zu S. 65, nur eine Seite daneben, wo bi als imaginäre Zahl angegeben wird (dtv-Atlas der).
Polarform z = |z| (cos phi + i sin phi)
x = |z| cos phi
- y = |z| sin phi
|z| = WURZEL(x^2 + y^2)
tan phi = y/x . x <> 0
Exponentialform z = |z| e^(i*ar(z)) mit arg(z) = 0, pi/2, pi, 3/2 pi.
e^(i*phi) = cos phi + i sin phi (Eulersche Formel)
e^-(i*phi) = cos phi - i sin phi (konjugiert)
_
Moivre-Formel (cos phi + i sin phi)^n = cos n*phi + i sin n*phi
_
i als Drehoperator
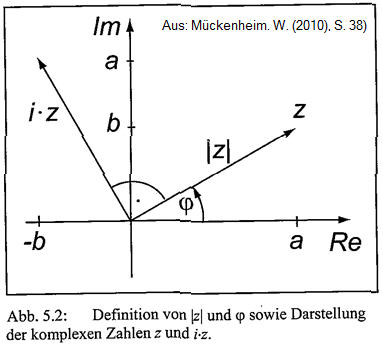
Die Multiplikation einer komplexen Zahl z mit i, i^2, i^3 dreht diese
in der Gaußschen komplexen Zahlenebene jeweils einen Quadranten gegen
den Uhrzeigersinn weiter. Wenn z=1 + i, dann ist z*i = -1 + 1i, z*i^2 =
-1 - 1i, z*i^3 = 1 - 1i. Das Schaubild zeigt eine Raute.
_
Exkurs: Existenz von i
Manchmal wird die Frage nach der Existenz von i diskutiert, was ich nicht so recht nachvollziehen konnte, weil doch unzweifelhaft viele Ausdrücke WURZEL(-a), a>0 tatsächlich z.B. in Gleichungen vorkommen. So gesehen stellte sich für mich nur die Frage, ob es - neben der ja schon seit ca. Mitte des 18. Jhds. längst erwiesenen praktischen Nützlichkeit von i - eine Ergebnislösung gibt.
Dittmann (1984), S. 21f: "In Abschnitt 2.1.1. stellten wir zunächst fest, daß es keine (reelle) Zahl gibt, deren Quadrat negativ ist, um gleich darauf in 2.1.2. eine Zahl, deren Quadrat — 1 sein soll, „einzuführen". Wie nun, wenn eine derartige Zahl grundsätzlich nicht existieren kann, wenn sie einen Widerspruch in sich darstellt? ... ... Dadurch, daß man für ein nichtexistierendes Objekt einen Buchstaben setzt und ihm einen Namen gibt, kann dies nicht in die Existenz erhoben werden."
Diese Aussagen von Dittmann führen auf eine andere mathematik-sprachliche Baustelle, die Frage mathematischer Existenz, die hier nicht weiter thematisiert werden soll, sondern demnächst eine eigene Seite erhalten wird. Tatsache ist aber natürlich, dass die bloße Zuordnung eines Buchstabens keinen sachlichen Erklärungswert hat. Da es ohne jeden Zweifel Qudratwurzeln negativer reeller Zahlen gibt, kann es meines Erachtens keine Frage der Existenz sein. Ob und wie sie lösbar sind, ist eine andere Frage. Wenn man definiert, dass Minus mal Minus im Reellen Plus ergibt, dann kann es im Reellen keine Lösung für WURZEL(-a), a > 0 geben, also auch nicht für WURZEL(-1).
Ueberlegungen zur effektiven Lösung WURZEL(-1)
i ist nur eine Abkürzung, ein Symbol, das Definiendum für WURZEL(-1). Man kann WURZEL(-1) durch i ersetzen und umgekehrt. Aber mit der bloßen Angabe i ist die ursprüngliche Aufgabe, eine Lösung oder Lösungen für WURZEL(-1) anzugeben, nicht gelöst. Anders und einfach gefragt: Was kommt denn nun heraus, wenn man die Quadrat-Wurzel aus einer negativen reellen Zahl, hier speziell WURZEL(-1) zieht? Merkwürdigerweise findet man diese Frage in den meisten Abhandlungen zu den komplexen Zahlen nicht beantwortet. Auch die newsgroup de.sci.mathematik zeigte sich hierzu nicht im Stande, so dass ich auf eigene Überlegungen angewiesen war.
Eigene Vorueberlegungen
Gesucht ist eine Zahl, deren Produkt -1 ergibt. Es liegt auf der Hand,
dass dies die Zahlen +1 und -1 sind, also zwei Zahlen vom gleichen Betrag.
Allgemein (+a) * (-a), a > 0. Als Lösung für WURZEL(-a), a >
0 bietet sich an (-1) * WURZEL(|-a|) = (-1) * WURZEL(a). Nach diesen Überlegungen
bestünde die Quadratzahl aus zwei dem Betrag nach gleichen Zahlen
mit unterschiedlichen Vorzeichen, wobei die Multiplikation aber dem Reellen
entlehnt ist. Berücksichtigt man die Multiplikationsregel für
die komplexen Zahlen (a,b)*(c,d) = ac-bd, ad + bc so
ergibt sich wie vorüberlegt:
(0 + 1) * (0 + 1) = 0 - 1, 0 + 0 = -1
(0 - 1) * (0 - 1) = 0 + 1, 0 + 0 = +1
Darstellung des Wurzelziehens aus imaginären Zahlen (14.08.2016)
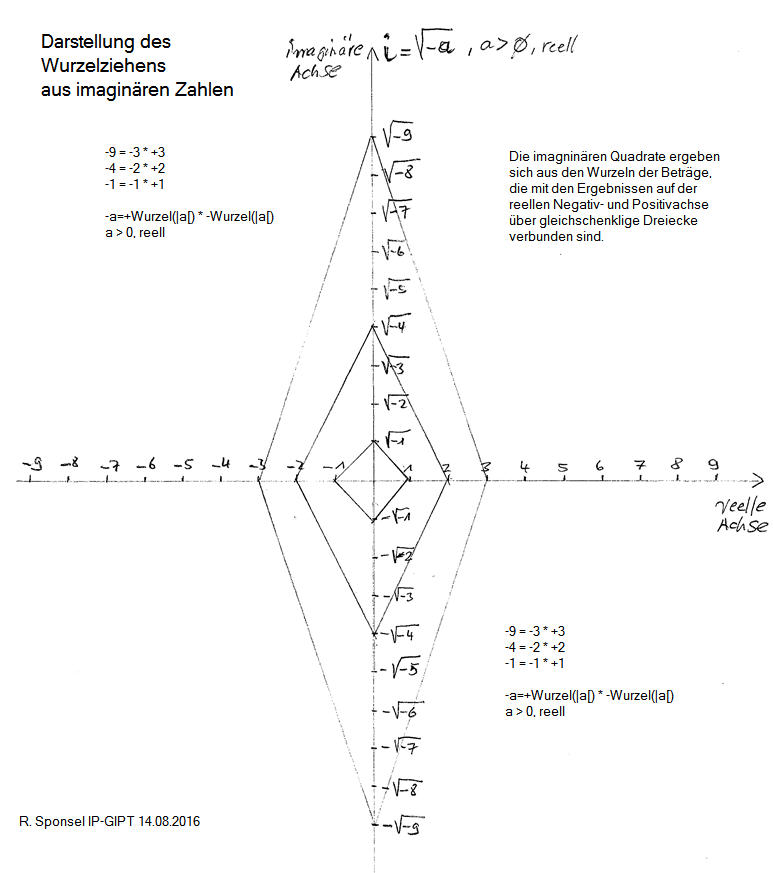
Die "Loesungen" für
x^2 + 1 = 0 bzw. allgemein
21.08.16 Die Mathematik lehrt: i = i und -i.
In Worten: Die Lösungen aus WURZEL(-1) lauten WURZEL(-1) und -WURZEL(-1).
Es hat ca. vier Wochen gedauert, bevor ich diese Aussage nun so formulieren
konnte. Inhaltlich akzeptieren kann ich die Lösungen nicht, weil sich
meine Vorstellung dagegen sperrt, dass das Ergebnis des Wurzel ziehens
zur gleichen Zahl führen kann wie die Wurzel selbst. Auch als ich
versuchte, mir mit der Analogie im Reellen, die erste Ableitung aus e^x
ist wiederum e^x zu helfen, wurde es nur wenig besser. Ich bin also noch
nicht durch.
23.08.16 Nur in einem Buch fand ich zunächst
die Frage beantwortet, was denn nun nach Einführung der komplexen
Zahlen, für x^2+1=0 herauskommt. Nämlich bei Mückenheim
(2010), S. 133:
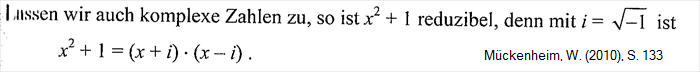
Das hatte mit meiner Irritation um den Begriff der "Lösung" zu
tun (> Zwischenstand-2 (1)). Ich war darauf
fixiert, was denn nun herauskommt, wenn man die Wurzel aus -1 tatsächlich
zieht.
- i als Loesung
bei Oberschelp (1976), S. 162 (Hinweis FF in dsm 19.7.16)

- Loesung
i und -i nach Fritzsche, K. (2016)

- _
Bartsch Loesung a^2=-a, a > 0, reell
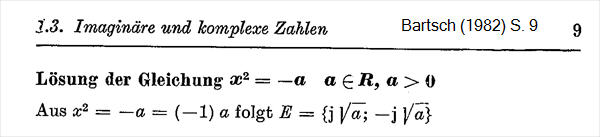
- Nach Dittmann (1981),
S. 20 ergibt sich für WURZEL(-1) = 1i und -1i.

Anmerkung: Das Sachregister enthält keinen Eintrag Exponentialdarstellung.
Nach Dittmann (1984), S. 23, Fußnote: "Man beachte: Der Imaginärteil
ist selbst eine reelle Zahl". Korrekt müsste es heißen: "Der
Imaginärteil in der geordneten Paardarstellung ist selbst eine reelle
Zahl".
_
Loesungen nach Kretzschmar
(2011)
Als Lösungen für WURZEL(-1) ergeben sich 1i und -1i.

_
i
und -i Wurzeln aus -1 nach Karpfinger

_
Uni
Regensburg i und -i

_
Spezielle
Lösung für Wurzel(-1) nach Wikipedia

Hier ist plötzlich - wie so oft - b verschwunden, nämlich
die 1.
_
Allgemeine Loesung
nach Wikipedia
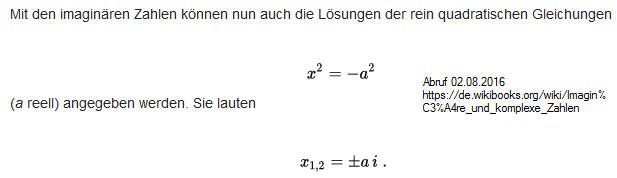
- Loesungen
quadratischer Gleichungen in C nach Lambacher Schweizer

_
Quadratwurzel ziehen
mit Matlab Studentenversion 5.3
- > Zum Gefühl bekommen Beispiele mit Matlab
(Stud 5.3).
| WURZEL(-1) mit Eingabe sqrt(0 + (-1)) führt zum Ergebnis
0 + 1.0000i. Das entspricht dem, was die MathematikerInnen sagen. Hier
ist i nicht nur ein Symbol, sondern wird auch als Lösung ausgegeben,
hier sogar mit dem reellen Faktor 1, was meist gar nicht gemacht wird (weil
viele wohl gewohnt sind, 1 wegzulassen). Allerdings fehlt hier das -i (>
i
und -i Wurzeln aus -1 nach Karpfinger).
Anmerkung: Mein erster Rechenansatz war falsch. Er rechnete nicht WURZEL(-1) sondern WURZEL(WURZEL(-1)), also WURZEL(i) mit dem Ergebnis 0.7071 + 0.7071i. |
Literatur (Auswahl)
- Bartsch, Hans Jochen (1982) Taschenbuch Mathematischer Formeln. 3. - 6. Auflage. Frankfurt: Deutsch.
- Behnke, H.; Remmert, R.; Steiner, H.G. & Tietz, H. (1964, Hrsg.). Mathematik 1. Frankfurt a.M.: Das Fischer Lexikon.
- Bronstein, L.N. & Semendjajew, K.A. (1981) Taschenbuch Mathematik Neubearbeitung. 20. Auflage. Frankfurt aM: Deutsch.
- Dittmann, Helmut (1981) Komplexe Zahlen. 4. Auflage. München: Bayerischer Schulbuch-Verlag.
- DIN-Taschenbuch 202 Formelzeichen, Formelsatz, mathematische Zeichen und Begriffe
- Engel, Joachim & Fest, Andreas (2016) Ausgabe: 3., erweiterte und überarbeitete Auflage. Berlin; Boston: de Gruyter. Hier vorletzte Auflage aus 2009 genutzt.
- Engesser, Hermann (1986). Der kleine Duden Mathematik. Mannheim: PI. [kein Eintrag Hauptwert]
- Engesser, Hermann & Scheid, Harald (1994, 5.A.). Duden. Rechnen und Mathematik. Das Lexikon für Schule und Praxis. Mannheim: Duden-Verlag. [kein Eintrag Hauptwert]
- Fritzsche, Klaus (2016) KomplexeZahlen (oder: ImaginareWelten) In (299-312) Tutorium Mathematik für Einsteiger. Berlin: Springer.
- Karpfinger, Christian (2014) Höhere Mathematik in Rezepten. Berlin: Springer.
- Kretzschmar, Frank (2011) Komplexe Zahlen für Dummies. Das Pocketbuch. Wiley. [S. 36, 113]
- Mückenheim, Wolfgang (2010) Die komplexen Zahlen. In (37-42): München: Oldenbourg. Mathematik für die ersten Semester. 2. A.
- Naas, J. & Schmid, H.L. (1972-74, Hrsg.). Mathematisches Wörterbuch mit Einbeziehung der theoretischen Physik Bd. I A-K, Bd. II. L-Z. Berlin und Leipzig: Akademie und Teubner.
- Nahin, Paul J. (1998) An Imaginary Tale: The Story of the Square Root of Minus One. Princeton, Oxford: Princeton University Press.
- Niederdrenk-Felgner, Cornelia (2004) Lambacher Schweizer - Themenhefte / Komplexe Zahlen1. April 2004
- Pieper, Herbert (1984) Die komplexen Zahlen : Theorie - Praxis - Geschichte. Auch: Deutsch-Taschenbücher; Bd. 44
- Reinhardt, Fritz & Soeder, Heinrich (1982 f). dtv-Atlas zur Mathematik. 2 Bde. München: dtv. [Wird anscheinend nicht mehr aufgelegt]
- Walz, G. (2003, Red.). Lexikon der Mathematik. 6 Bde.: Verlag: Elsevier - Spektrum Akademischer Verlag. Hier Bd. 2 und 3 genutzt.
Links (Auswahl: beachte)
Es finden sich sehr viele Seiten zu den komplexen und imaginären Netz. Ich verzichte zur Minimierung der Linkfehler 404 auf Direkthinweise.
Glossar, Anmerkungen und Fußnoten
1) GIPT= General and Integrative Psychotherapy, internationale Bezeichnung für Allgemeine und Integrative Psychotherapie.
__
Analytische Funktion Vereinfacht: differenzierbar in einer Umgebung und als Potenzreihe darstellbar. Andere Bezeichnungen: holomorph, regulär. Orientiert an DMuR 1994, Analytische Funktion.
__
Existenz
Schwieriger, vieldeutiger, philosophischer und wissenschaftlicher Ausdruck. Existenz ist ein vieldeutiges Homonym. Es ist daher sinnvoll, Kennzeichnungen für die verschiedenen Hauptbedeutungen zu entwickeln, z.B. wie folgt:
- Existenz? := ohne nähere Spezifikation. Die Bedeutung muss aus dem Kontext erschlossen werden.
- Existenzallt := alltagssprachliche Existenz,
- Existenzbild := bildungssprachliche Existenz,
- Existenzbiol := biologische Existenz
- Existenzchem := chemische Existenz,
- Existenzjur := juristische Existenz (Probleme der Generalklauseln und der Konstrukte überhaupt: die juristischen Beweismethoden: Augenschein, Urkunde, Sachverständige, Zeugen, Indizien, ...)
- Existenzlog := Logische Existenz
- Existenzmath := mathematische. In welcher Weise existieren Zahlen? Sind natürliche Zahlen realer als imaginäre?
- Existenzont := ontologische Existenz,
- Existenzphysik := physikalische Existenz,
- Existenzpol := politische Existenz (z.B. Anerkennung von Menschen (Personalausweis), Institutionen und Staaten)
- Existenzpsychol := psychologische Existenz (Normative-, Wunsch-, Phantasie-, Realwelt)
- Existenzspra := sprachliche Existenz (nicht jedes Wort muss auch wirklich etwas bedeuten, ein ganz gefährlicher Fallstrick in vielen Auseinandersetzungen und Diskussionen)
- Existenzreli := religiöse Existenz
- Existenztech := technische Existenz
__
Funktionentheorie "Theorie der komplexen Funktionen einer oder mehrerer komplexer Variabler (t Funktion, > komplexe Zahlen). Mit Hilfe des Betrags einer komplexen Zahl werden Begriffe wie Stetigkeit und Differenzierbarkeit einer Funktion einer komplexen Variablen ähnlich wie bei einer Funktion einer reellen Variablen definiert. Wesentlicher Teil der Funktionentheorie ist die Theorie der > analytischen Funktionen." DRuM 1994, S. 197.
__
Zum Gefuehl bekommen Beispiele mit Matlab (Stud 5.3)
| 1+i = 1.0000 + 1.0000i
1-i = 1.0000 - 1.0000i 1*i = 0 + 1.0000i 1/i = 0 - 1.0000i 0 - i = 0 - 1.0000i
sqrt(sqrt(-1)) = 0.7071 + 0.7071i
|
0 + sqrt(-4) = 0 + 2.0000i
0 + sqrt(-9) = 0 + 3.0000i 0 + sqrt(-16) = 0 + 4.0000i 0 + sqrt(-25) = 0 + 5.0000i (0+3i)*(0+4i) = -12 (0+3i)*(0+4i)*i = 0 -12.0000i 0 + sqrt(i) = 0.7071 + 0.7071i
|
e^(i*pi) = -1.0000 + 0.0000i = -1
e^(i*pi/2) = 0 + 1.0000i e^i = 0.5403 + 0.8415i e^pi = 23.1407 cos(30) + sin(60) =
Wurzel(-1) = 0 + 1.0000i
|
Weitere Materialien zu komplexe Zahlen
- Komplexe Zahlen im Lexikon
der Mathematik Bd. 3, Spektrum 2004

Komplexe Zahlen aus einem Schnupperkurs

Standort: Komplexe Zahlen.
*
Überblick Arbeiten zur Theorie, Definitionslehre, Methodologie, Meßproblematik, Statistik und Wissenschaftstheorie besonders in Psychologie, Psychotherapie und Psychotherapieforschung.
*
| Suchen in der IP-GIPT,
z.B. mit Hilfe von "google": <suchbegriff>
site: www.sgipt.org
z.B. Wissenschaft site: www.sgipt.org. |
Dienstleistungs-Info.
*
Zitierung
Sponsel, R. (DAS). Die Sprache der Mathematik am Beispiel komplexe & imaginäre Zahlen aus der Sicht eines mathematisch interessierten Laien. Internet Publikation für Allgemeine und Integrative Psychotherapie IP-GIPT. Erlangen: https://www.sgipt.org/wisms/mathe/sprache/komplexeZ/komplexeZ.htm
Copyright & Nutzungsrechte
Diese Seite darf von jeder/m in nicht-kommerziellen Verwertungen frei aber nur original bearbeitet und nicht inhaltlich verändert und nur bei vollständiger Angabe der Zitierungs-Quelle benutzt werden. Das direkte, zugriffsaneignende Einbinden in fremde Seiten oder Rahmen ist nicht gestattet, Links und Zitate sind natürlich willkommen. Sofern die Rechte anderer berührt sind, sind diese dort zu erkunden. Sollten wir die Rechte anderer unberechtigt genutzt haben, bitten wir um Mitteilung. Soweit es um (längere) Zitate aus ... geht, sind die Rechte bei/m ... zu erkunden oder eine Erlaubnis einzuholen.
Ende_ Komplexe & imaginäre Zahlen__Rel. Aktuelles _Überblick_Überblick Wissenschaft _Rel. Beständiges_ Titelblatt_ Konzept_ Archiv_Region_Service iec-verlag__Wichtige Hinweise zu Links und Empfehlungen_ Mail: sekretariat@sgipt.org_
sprachlich korrigiert: 19.08.16, 15.08.2016 irs
Änderungen Kleinere Änderungen werden nicht extra ausgewiesen; wird gelegentlich überarbeitet und ergänzt.
11.09.16 i als Loesung bei Oberschelp (1976). * Relativierende Einfügung "zunächst" bei Mückenheim.
04.09.16 Zwischenstand-2. * Loesungen quadratischer Gleichungen in C nach Lambacher Schweizer. * i als Definition nach Lambacher Schweizer *
23.08.16 Ergebnis für x^2+1=0 nach Mückenheim (2010), S. 133
21.08.16 Zwischenstand.
20.08.16 Exkurs Vorüberlegung zum Begriff der Einheit. * Lösung x^2=-1 Uni Regensburg * Fritzsche, K. (2016) * Rottmann 1991 *
19.08.16 Zum Geleit * Sprachregelung komplexe Zahlen nach DIN 1302, 4.-4.6. * Kritik. * Kritik dtv-Atlas * Imaginärteil b bzw. bi im Duden Rechnen und Mathematik * Bartsch Lösung a^2=-a, a > 0, reell. * Zusammenfassung-2 Ergebnisse der Sichtung mathematischer Texte. Was heißt "Imaginaerteil "? Was "ist" i und was ist WURZEL(-1)? Die Loesung imaginaerer Quadratwurzeln.
14.08.16 Darstellung des Wurzelziehens aus imaginären Zahlen * i als Drehoperator: Abb. 5.2 aus Mückenheim, W. (2010), S. 38
13.08.16 Fehlerkorrekturen. Kretzschmars Lösung.
12.08.16 Vorläufige Fassung zur Kritik ins Netz gestellt.
05.07.16 Angelegt und nach und nach entwickelt. Immer mal wieder ein paar Stunden.